【题目】如图,已知点A、C在反比例函数y= ![]() 的图象上,点B,D在反比例函数y=
的图象上,点B,D在反比例函数y= ![]() 的图象上,a>b>0,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=
的图象上,a>b>0,AB∥CD∥x轴,AB,CD在x轴的两侧,AB= ![]() ,CD=
,CD= ![]() ,AB与CD间的距离为6,则a﹣b的值是 .
,AB与CD间的距离为6,则a﹣b的值是 . 
参考答案:
【答案】3
【解析】解:设点A、B的纵坐标为y1 , 点C、D的纵坐标为y2 , 则点A( ![]() ,y1),点B(
,y1),点B( ![]() ,y1),点C(
,y1),点C( ![]() ,y2),点D(
,y2),点D( ![]() ,y2).
,y2).
∵AB= ![]() ,CD=
,CD= ![]() ,
,
∴2×| ![]() |=|
|=| ![]() |,
|,
∴|y1|=2|y2|.
∵|y1|+|y2|=6,
∴y1=4,y2=﹣2.
连接OA、OB,延长AB交y轴于点E,如图所示.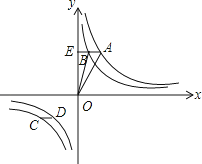
S△OAB=S△OAE﹣S△OBE= ![]() (a﹣b)=
(a﹣b)= ![]() ABOE=
ABOE= ![]() ×
× ![]() ×4=
×4= ![]() ,
,
∴a﹣b=2S△OAB=3.
所以答案是:3.
【考点精析】本题主要考查了反比例函数的性质的相关知识点,需要掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=
 ,BC=
,BC=  ,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于点F,则
,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于点F,则 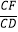 = .
= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.
(1)△BEM与△AEC全等吗?请说明理由;
(2)BM与AC相等吗?请说明理由;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为
 ,
, ,
, ,
, ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为 .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为 ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某运动员在一场篮球比赛中的技术统计如表所示:
技术
上场时间(分钟)
出手投篮(次)
投中
(次)罚球得分
篮板
(个)助攻(次)
个人总得分
数据
46
66
22
10
11
8
60
注:表中出手投篮次数和投中次数均不包括罚球.
根据以上信息,求本场比赛中该运动员投中2分球和3分球各几个. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD的对角线AC、BD交于点O,若OE=OF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)求证:四边形DEBF是平行四边形;
(3)若OD=OE=OF,则四边形DEBF是什么特殊的四边形,请证明.

相关试题

