搜索
【题目】如图，矩形ABCD中，AB= 
，BC= 
，点E在对角线BD上，且BE=1.8，连接AE并延长交DC于点F，则 
= ． 
参考答案：
【答案】
【解析】解：∵四边形ABCD是矩形，
∴∠BAD=90°，又AB= 
，BC= 
，
∴BD= 
=3，
∵BE=1.8，
∴DE=3﹣1.8=1.2，
∵AB∥CD，
∴ 
= 
，即 
= 
，解得，DF= 
，则CF=CD﹣DF= 
，∴ 
= 
= ，
所以答案是： ．
【考点精析】通过灵活运用矩形的性质和相似三角形的判定与性质，掌握矩形的四个角都是直角，矩形的对角线相等；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图□ABCD的对角线AC，BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=600，AB=
BC，连接OE ．下列 结论：①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=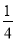
BC 成立的个数有（ ）
A．1个 B．2个 C．3个 D．4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：△ABC，∠A、∠B、∠C之和为多少？为什么？
解：∠A+∠B+∠C=180°
理由：作∠ACD=∠A，并延长BC到E
∵∠ACD=∠ （已作）
AB∥CD（ ）
∴∠B= （ ）
而∠ACB+∠ACD+∠DCE=180°
∴∠ACB+ + =180°（ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：
①AD⊥BD；②∠AOC=∠AEC；③CB平分∠ABD；④AF=DF；⑤BD=2OF；⑥△CEF≌△BED，其中一定成立的是（ ）
A.②④⑤⑥
B.①③⑤⑥
C.②③④⑥
D.①③④⑤ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图所示，△ABC中，∠ABC=45°，高AE与高BD交于点M，BE=4，EM=3．
（1）△BEM与△AEC全等吗？请说明理由；
（2）BM与AC相等吗？请说明理由；
（3）求△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AM∥BN，∠A=80°，点P是射线AM上动点（与A不重合），BC、BD分别平分∠ABP和∠PBN，交射线AM于C、D．
（1）求∠CBD的度数；
（2）当点P运动时，那么∠APB：∠ADB的度数比值是否随之发生变化？若不变，请求出这个比值；若变化，请找出变化规律；
（3）当点P运动到使∠ACB=∠ABD时，求∠ABC的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点A、C在反比例函数y=
的图象上，点B，D在反比例函数y= 
的图象上，a＞b＞0，AB∥CD∥x轴，AB，CD在x轴的两侧，AB= 
，CD= 
，AB与CD间的距离为6，则a﹣b的值是 ． 
相关试题
