【题目】如图,AB⊥BC,DC⊥BC,若∠DBC=45°,∠A=70°,求∠D,∠AED,∠BFE的度数.

参考答案:
【答案】∠D=45°;∠AED=70°;∠BFE=115°.
【解析】
根据直角三角形两锐角互余列式求解即可得到∠D,根据在同一平面内垂直于同一直线的两直线互相平行可得AB∥CD,再根据两直线平行,内错角相等可得∠AED=∠A,然后根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BFE=∠D+∠AED.
∵DC⊥BC,∠DBC=45°,∴∠D=90°﹣∠DBC=90°﹣45°=45°;
∵AB⊥BC,DC⊥BC,∴AB∥DC,∴∠AED=∠A=70°;
在△DEF中,∠BFE=∠D+∠AED=45°+70°=115°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠B=90°,O是AB上的一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D.若AD=2
 , 且AB、AE的长是关于x的方程x2﹣8x+k=0的两个实数根.
, 且AB、AE的长是关于x的方程x2﹣8x+k=0的两个实数根.
(1)求⊙O的半径.
(2)求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知等腰三角形的一边长等于8cm,一边长等于9cm,求它的周长;
(2)等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的边BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点E.
(1)如图1,若∠ABC=90°,求证:OE∥AC;
(2)如图2,已知AB=AC,若sin∠ADE= , 求tanA的值.
, 求tanA的值.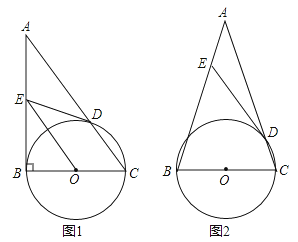
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是以AB为直径的⊙O上的一点,BD与过点C的切线互相垂直,垂足为点D.
(1)求证:BC平分∠DBA;
(2)若CD=6,BC=10,求⊙O的半径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC,交AB于E,则下列结论一定正确的是( )
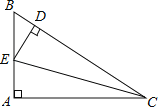
A. AE=BE B. DB=DE C. AE=BD D. ∠BCE=∠ACE
相关试题

