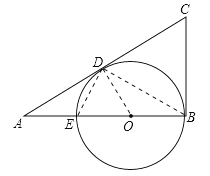
【题目】如图,∠B=90°,O是AB上的一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D.若AD=2![]() , 且AB、AE的长是关于x的方程x2﹣8x+k=0的两个实数根.
, 且AB、AE的长是关于x的方程x2﹣8x+k=0的两个实数根.
(1)求⊙O的半径.
(2)求CD的长.
参考答案:
【答案】解:(1)连接OD、DE、DB,设⊙O半径为r,
∵CD为⊙O切线,∴∠ODA=90°,
∵BE为⊙O直径,∴∠BDE=90°,
∴∠ADE=∠BDO,
∵OB=OD,∴∠OBD=∠ODB,
∵∠DAE=∠BAD,
∴△ADE∽△ABD,
∴![]() ,
,
∴ABAE=![]() ,
,
∵AB、AE的长是关于x的方程x2﹣8x+k=0的两个实数根,
∴k=12,
解方程x2﹣8x+12=0得:两个实数根为:2和6,
∴设半径的长为r,
可得半径r=![]() ×(6﹣2)=2;
×(6﹣2)=2;
(2)∵∠B=90°,
∴CB为⊙O切线,
∴CD=CB,
∴CB2+AB2=AC2 ,
∴CD2+62=(2![]() +CD)2 ,
+CD)2 ,
∴CD=2![]() .
.
答:CD的长度为2![]() .
.
【解析】(1)根据切线长定理得出ABAE的长=12,进而得出k的值,设半径的长为r,再代入切线长定理解答即可;
(2)根据切线长定理,即可得出CD=CB,由勾股定理得CD的长即可.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )

A. 8 B. 16 C. 24 D. 32
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BE是圆O的直径,A在EB的延长线上,AP为圆O的切线,P为切点,弦PD垂直于BE于点C.
(1)求证:∠AOD=∠APC;
(2)若OC:CB=1:2,AB=6,求圆O的半径及tan∠APB.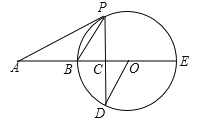
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AE⊥AB且AE=AB,BC⊥CD且BC=CD,按照图中所标注的数据,则图中阴影部分图形的面积S等于( )

A. 50 B. 62 C. 65 D. 68
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知等腰三角形的一边长等于8cm,一边长等于9cm,求它的周长;
(2)等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的边BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点E.
(1)如图1,若∠ABC=90°,求证:OE∥AC;
(2)如图2,已知AB=AC,若sin∠ADE= , 求tanA的值.
, 求tanA的值.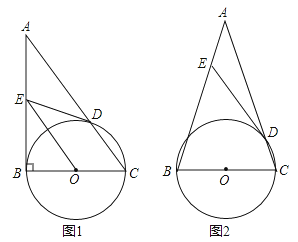
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,DC⊥BC,若∠DBC=45°,∠A=70°,求∠D,∠AED,∠BFE的度数.

相关试题

