【题目】如图,以△ABC的边BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点E.
(1)如图1,若∠ABC=90°,求证:OE∥AC;
(2)如图2,已知AB=AC,若sin∠ADE=![]() , 求tanA的值.
, 求tanA的值.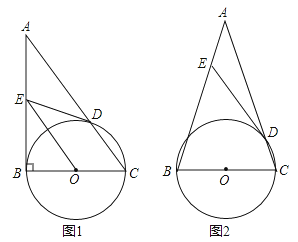
参考答案:
【答案】解:(1)证明:连结OD,如图1,
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
在Rt△OBE和Rt△ODE中,![]()
∴Rt△OBE≌Rt△ODE,
∴∠1=∠2,
∵OC=OD,
∴∠3=∠C,
而∠1+∠2=∠C+∠3,
∴∠2=∠C,
∴OE∥AC;
(2)解:连结OD,作OF⊥CD于F,DH⊥OC于H,如图2,
∵AB=AC,OC=OD,
而∠ACB=∠OCD,
∴∠A=∠COD,
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
∴∠ADE+∠ODF=90°,
而∠DOF+∠ODF=90°,
∴∠ADE=∠DOF,
∴sin∠DOF=sin∠ADE=![]() ,
,
在Rt△DOF中,sin∠DOF=![]() =
=![]() ,
,
设DF=x,则OD=3x,
∴OF=![]() =2
=2![]() x,DF=CF=x,OC=3x,
x,DF=CF=x,OC=3x,
∵![]() DHOC=
DHOC=![]() OFCD,
OFCD,
∴DH=![]() =
=![]() x,
x,
在Rt△ODH中,OH=![]() =
=![]() x,
x,
∴tan∠DOH=![]() =
=![]() =
=![]() ,
,
∴tan∠A=![]() .
.

【解析】(1)连结OD,如图1,根据切线的性质得∠ODE=90°,再证明Rt△OBE≌Rt△ODE得到∠1=∠2,加上∠3=∠C,则利用三角形外角性质可得∠2=∠C,然后根据平行线的判定可判断OE∥AC;
(2)连结OD,作OF⊥CD于F,DH⊥OC于H,如图2,根据等腰三角形的性质和三角形内角和定理,由AB=AC,OC=OD,∠ACB=∠OCD可得∠A=∠COD,根据切线的性质得∠ODE=90°,则∠ADE+∠ODF=90°,
而∠DOF+∠ODF=90°,利用等角的余角相等得∠ADE=∠DOF,于是有sin∠DOF=sin∠ADE=![]() , 在Rt△DOF中,根据正弦的定义得到
, 在Rt△DOF中,根据正弦的定义得到![]() =
=![]() , 则可设DF=x,则OD=3x,利用勾股定理计算出OF=2
, 则可设DF=x,则OD=3x,利用勾股定理计算出OF=2![]() x,DF=CF=x,OC=3x,接着可运用面积法计算出DH=
x,DF=CF=x,OC=3x,接着可运用面积法计算出DH=![]() span>x,然后在Rt△ODH中用勾股定理计算出OH=
span>x,然后在Rt△ODH中用勾股定理计算出OH=![]() x,再根据正切的定义求解即可.
x,再根据正切的定义求解即可.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AE⊥AB且AE=AB,BC⊥CD且BC=CD,按照图中所标注的数据,则图中阴影部分图形的面积S等于( )

A. 50 B. 62 C. 65 D. 68
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠B=90°,O是AB上的一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D.若AD=2
 , 且AB、AE的长是关于x的方程x2﹣8x+k=0的两个实数根.
, 且AB、AE的长是关于x的方程x2﹣8x+k=0的两个实数根.
(1)求⊙O的半径.
(2)求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知等腰三角形的一边长等于8cm,一边长等于9cm,求它的周长;
(2)等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,DC⊥BC,若∠DBC=45°,∠A=70°,求∠D,∠AED,∠BFE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是以AB为直径的⊙O上的一点,BD与过点C的切线互相垂直,垂足为点D.
(1)求证:BC平分∠DBA;
(2)若CD=6,BC=10,求⊙O的半径长.
相关试题

