【题目】【问题背景】
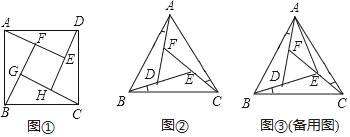
如图①所示,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
【类比研究】
如图②所示,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合).
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)连结AE,若AF=DF,AB=7,求△DEF的边长.
参考答案:
【答案】(1)△ABD≌△BCE≌△CAF;理由见解析;(2)△DEF是正三角形;理由见解析;(3)![]()
【解析】分析:(1)由正三角形的性质得出∠CAB=∠ABC=∠BCA=60°,AB=BC,证出∠ABD=∠BCE,由ASA证明△ABD≌△BCE即可;
(2)由全等三角形的性质得出∠ADB=∠BEC=∠CFA,证出∠FDE=∠DEF=∠EFD,即可得出结论;
(3)先判断出AF=FD=EF,进而得出∠FAE=∠FEA=30°,即:∠DEA=90°,再用勾股定理得出AE,即可得出结论.
详解:(1)△ABD≌△BCE≌△CAF;理由如下:
∵△ABC是正三角形,
∴∠CAB=∠ABC=∠BCA=60°,AB=BC,
∵∠ABD=∠ABC-∠CBE,∠BCE=∠ACB-∠ACF,∠CBE=∠ACF,
∴∠ABD=∠BCE,
在△ABD和△BCE中,
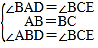 ,
,
∴△ABD≌△BCE(ASA);
同理:△ABD≌CAF,
即:△ABD≌△BCE≌△CAF
(2)△DEF是正三角形;理由如下:
∵△ABD≌△BCE≌△CAF,
∴∠ADB=∠BEC=∠CFA,
∴∠FDE=∠DEF=∠EFD,
∴△DEF是正三角形;
(3)∵△DEF是正三角形,
∴∠DFE=∠FDE=60°,
又AF=FD,
∴AF=FD=EF,
∴∠FAE=∠FEA=30°,
∴∠DEA=90°,
设DE=x,则AD=BE=2x,
在Rt△ADE中,AE2=AD2-DE2=3x2,
在Rt△ABE中,AB=7,AB2=BE2+AE2,
即,49=4x2+3x2,
∴x=-![]() (舍)或x=
(舍)或x=![]() ,
,
∴△DEF的边长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
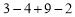 .
.(2)
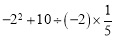 .
.(3)
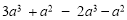 .
.(4)
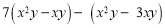 .
.(5)解方程
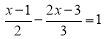
(6)解方程组
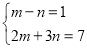
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D的坐标为(2,0),E为AB上的点,当△CDE的周长最小时,点E的坐标为( )
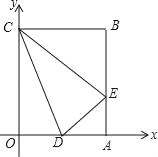
A. (1,3) B. (3,1) C. (4,1) D. (3,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,自行车链条每节链条的长度为2.5cm ,交叉重叠部分的圆的直径为0.8cm.
(1)尝试: 2节链条总长度是________
 , 3节链条总长度是________
, 3节链条总长度是________  .
.(2)发现:用含
 的代数式表示
的代数式表示 节链条总长度是________. ( 要求填写最简结果)
节链条总长度是________. ( 要求填写最简结果)(3)应用:如果某种型号自行车链条总长度为
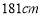 ,则它是由多少节这样的链条构成的?
,则它是由多少节这样的链条构成的?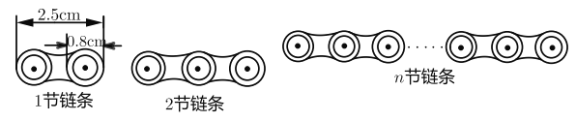
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点
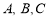 在同一条直线上,点
在同一条直线上,点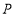 为线段
为线段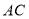 的中点,点
的中点,点 为线段
为线段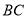 的中点.
的中点.(1)如图1 ,当点
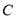 在线段
在线段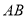 上时.
上时.①若
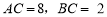 ,则线段
,则线段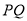 的长为_______.
的长为_______.②若点
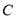 为线段
为线段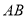 上任意一点,
上任意一点, 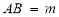 ,则线段
,则线段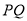 的长为_______. ( 用含
的长为_______. ( 用含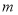 的代数式表示)
的代数式表示)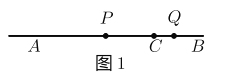
(2)如图2 ,当点
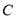 不在线段
不在线段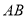 上时,若
上时,若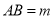 ,求
,求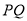 的长(用含
的长(用含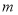 的代数式表示) .
的代数式表示) .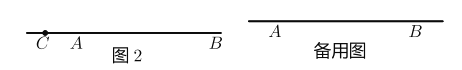
(3)如图,已知
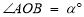 ,作射线
,作射线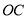 ,若射线
,若射线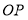 平分
平分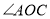 ,射线
,射线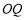 平分
平分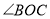 .
.①当射线
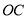 在
在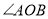 的内部时,则
的内部时,则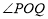 =________°.
=________°.②当射线
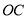 在
在 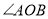 的外部时,则
的外部时,则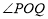 =_______°. ( 用含
=_______°. ( 用含 的代数式表示) .
的代数式表示) .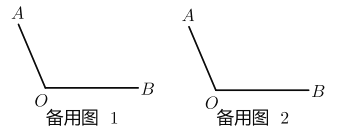
-
科目: 来源: 题型:
查看答案和解析>>【题目】北国超市销售每台进价分别为400元、350元的
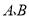 两种型号的豆浆机.下表是近两周的销售情况:
两种型号的豆浆机.下表是近两周的销售情况:销售数量:
销售时段
销售数量
销售收入
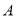 种型号
种型号 种型号
种型号第一周
3台
5台
3500元
第二周
4台
10台
6000元
(进价、售价均保持不变,利润=销售收入-进价)
(1)求
 两种型号的豆浆机的销售单价;
两种型号的豆浆机的销售单价;(2 )若第三周该超市采购这两种型号的豆浆机共20台, 并且B型号的台数比A型号的台数的2倍少1 ,如果这20台豆浆机全部售出,求这周销售的利润;
(3)若恰好用8000元采购这两种型号的豆浆机,问有哪几种进货方案? ( 要求两种型号都要采购)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,将ABCD放置在第一象限,且AB∥x轴,直线y=﹣x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2,那么ABCD面积为_____.
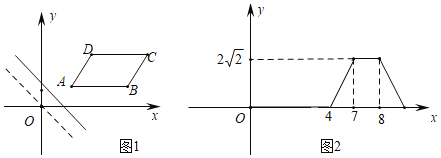
相关试题

