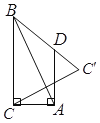
【题目】如图,在![]() 中,
中,![]() ,作
,作![]() 点关于直线
点关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() .过
.过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,若
,若![]()
![]() ,
,![]()
![]() ,则
,则![]() 的周长是_____
的周长是_____ ![]() .
.
参考答案:
【答案】![]()
【解析】
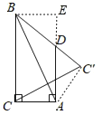
由勾股定理可求出AB的长,根据轴对称,可得到全等三角形,通过作辅助线构造全等三角形,从而得到AD=BD,设未知数,由勾股定理列方程,求出AD,进而计算三角形的周长.
过点B作BE⊥AD,交AD的延长线于点E,连接AC′,则∠E=90![]() ,
,
∵C、C'关于直线AB对称,
∴△ABC≌△ABC′,
∴AC=AC′=4,BC=BC′=8,∠BCA=∠BC′A=90![]() =∠E,
=∠E,
∴四边形ACBE是矩形,
∴BE=AC=4,
∵∠BDE=∠ADC′
∴△BDE≌△ADC′(AAS),
∴BD=AD,
设BD=x,则DE=8x,
在Rt△BDE中,由勾股定理得:x2=(8x)2+42,
解得:x=5,即:AD=BD=5,
在Rt△ABC中,AB=![]() =
=![]() ,
,
△ABD的周长=AB+BD+AD=![]() +5+5=
+5+5=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
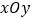 中,直线
中,直线 与
与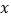 轴、
轴、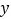 轴分别交于点
轴分别交于点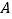 ,
,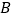 ,抛物线
,抛物线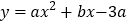 经过点
经过点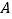 ,将点
,将点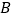 向右平移5个单位长度,得到点
向右平移5个单位长度,得到点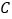 .
.(1)求点
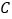 的坐标;
的坐标;(2)求抛物线的对称轴;
(3)若抛物线与线段
 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求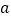 的取值范围.
的取值范围. -
科目: 来源: 题型:
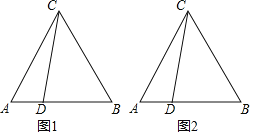
查看答案和解析>>【题目】已知△ABC为等边三角形,点D是线段AB上一点(不与A、B重合).将线段CD绕点C逆时针旋转60°得到线段CE.连结DE、BE.
(1)依题意补全图1并判断AD与BE的数量关系.
(2)过点A作AF⊥EB交EB延长线于点F.用等式表示线段EB、DB与AF之间的数量关系并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足
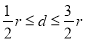 ,则称点P为⊙O的“随心点”.
,则称点P为⊙O的“随心点”.
(1)当⊙O的半径r=2时,A(3,0),B(0,4),C(
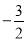 ,2),D(
,2),D(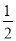 ,
,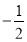 )中,⊙O的“随心点”是 ;
)中,⊙O的“随心点”是 ;(2)若点E(4,3)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=2时,直线y=- x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在家乡的楼顶上
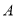 处测得池塘的一端
处测得池塘的一端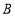 处的俯角为
处的俯角为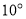 ,测得池塘
,测得池塘 处的俯角
处的俯角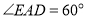 ,
,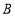 、
、 、
、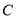 三点在同一水平直线上.已知楼高
三点在同一水平直线上.已知楼高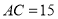 米,求池塘宽
米,求池塘宽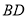 为多少米?(参考数据:
为多少米?(参考数据: ,
,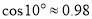 ,
, 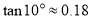 ,
,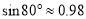 ,
,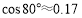 ,
, 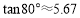 ,
,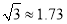 .结果保留一位小数.)
.结果保留一位小数.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年世界杯足球赛的“大力神杯”系列纪念品是中国制造.某商店用10000元购进一批“大力神杯”钥匙扣进行销售,很快销售一空.然后商店又用24000元购进这种钥匙扣,所购数量是第一批购进数量的2倍,但每个钥匙扣的价格比第一批的价格多了2元.
(1)该商店第一批购进的钥匙扣单价是多少元?
(2)若该商店第一、二批购进的钥匙扣都按相同的标价出售,并且全部售完,要使利润不低于20%,则每个钥匙扣的标价至少是多少元?
(3)在销售第二批钥匙扣时发现,若以每个15元价格出售,可全部售完.每涨价1元,销售量减少100件,剩余钥匙扣以每个10元价格全部售出.设该商店在销售第二批钥匙扣所获利润为P元,销售单价为m元,求P与m的函数关系式,并求出利润P最大时m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
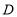 是⊙
是⊙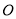 上一点,点
上一点,点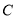 在直径
在直径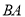 的延长线上,且
的延长线上,且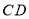 是⊙
是⊙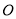 的切线,
的切线,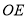 ∥
∥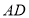 交
交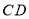 的延长线于点
的延长线于点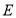 ,连结
,连结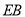 .
.(1) 求证:
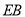 是⊙
是⊙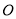 的切线.
的切线.(2) 若
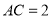 ,
,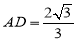 ,求⊙
,求⊙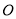 的半径.
的半径.
相关试题

