搜索
【题目】已知线段AB=5cm，点C为直线AB上一点，且BC=3cm，则线段AC的长是（ ）
A.2cm
B.8cm
C.9cm
D.2cm或8cm
参考答案：
【答案】D
【解析】解：本题有两种情形：
①当点C在线段AB上时，如图1，
∵AC=AB﹣BC，
又∵AB=5cm，BC=3cm，
∴AC=5﹣3=2cm；
②当点C在线段AB的延长线上时，如图2，
∵AC=AB+BC，
又∵AB=5cm，BC=3cm，
∴AC=5+3=8cm．
综上可得：AC=2cm或8cm．
故选D．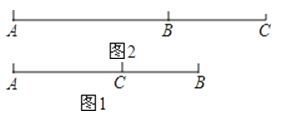
【考点精析】利用两点间的距离对题目进行判断即可得到答案，需要熟知同轴两点求距离，大减小数就为之．与轴等距两个点，间距求法亦如此．平面任意两个点，横纵标差先求值．差方相加开平方，距离公式要牢记．
-
科目： 来源： 题型：
查看答案和解析>>【题目】a、b为实数，在数轴上的位置如图，求|a﹣b|+
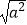的值．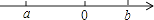 
-
科目： 来源： 题型：
查看答案和解析>>【题目】平面直角坐标系中，点P（x，y）的横坐标x的绝对值表示为|x|，纵坐标y的绝对值表示为|y|，我们把点P（x，y）的横坐标与纵坐标的绝对值之和叫做点P（x，y）的勾股值，记为「P」，即「P」=
+
．（其中的“+”是四则运算中的加法）（1）求点A（﹣1，3），B（
，
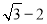）的勾股值「A」、「B」；（2）点M在反比例函数
的图象上，且「M」=4，求点M的坐标；（3）求满足条件「N」=3的所有点N围成的图形的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】以下各组数据为三角形的三边长，能构成直角三角形的是( )
A. 2，2，4 B. 2，3，4 C. 2，2，1 D. 4，5，3
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠AOM与∠MOB互为余角，且∠BOC=30°，OM平分∠AOC，ON平分∠BOC．
（1）求∠MON的度数；
（2）如果已知中∠AOB=80°，其他条件不变，求∠MON的度数；
（3）如果已知中∠BOC=60°，其他条件不变，求∠MON的度数；
（4）从（1）、（2）、（3）中你能看出有什么规律． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图：四边形ABCD中，AB=CB=
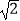，CD=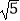 
，DA=1，且AB⊥CB于B．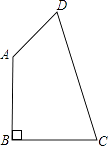
试求：
（1）∠BAD的度数；
（2）四边形ABCD的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如果点M、N在数轴上分别表示实数m,n,在数轴上M,N两点之间的距离表示为MN=m-n(m＞n)或n-m(m＜n)或︱m-n︱．利用数形结合思想解决下列问题：
已知数轴上点A与点B的距离为16个单位长度，点A在原点的左侧，到原点的距离为26个单位长度，点B在点A的右侧，点C表示的数与点B表示的数互为相反数，动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．
（1）点A表示的数为 ， 点B表示的数为 ， 点C表示的数为 ．
（2）用含t的代数式表示P到点A和点C的距离： PA= ， PC= ．
（3）当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动， Q点到达C点后，再立即以同样的速度返回，运动到终点A．
①在点Q向点C运动过程中，能否追上点P?若能，请求出点Q运动几秒追上．
②在点Q开始运动后，P、Q两点之间的距离能否为2个单位？如果能，请求出此时点P表示的数；如果不能，请说明理由．
相关试题
