【题目】如图,![]() 中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①
中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①![]() ;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若
;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若![]() ,则
,则![]() ;其中正确的有( )
;其中正确的有( )

A. 2个B. 3个C. 4个D. 5个
参考答案:
【答案】D
【解析】
利用SAS可证明△ABE≌△ACD,判断①正确;根据全等三角形的性质以及邻补角定义可得∠BDO=∠BEC,继而利用AAS证明△BOD≌△COE,可得OD=OE,BO=OC,判断③正确;利用SSS证明△AOD≌△AOE,可得AO平分∠BAC,判断②正确,继而根据等腰三角形三线合一的性质可判断④正确,根据三角形的高相等时,两三角形的面积比就是底边之比,通过推导可判断⑤正确.
在△ABE与△ACD中,
 ,
,
∴△ABE≌△ACD,故①正确;
∴∠AEB=∠ADC,
∴∠BDO=∠BEC,
∵AB=AC,AD=AE,∴BD=CE,
在△BOD与△COE中,
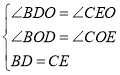 ,
,
∴△BOD≌△COE,
∴OD=OE,BO=OC,故③正确;
在△AOD与△AOE中,
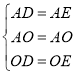 ,
,
∴△AOD≌△AOE,
∴∠DAO=∠EAO,
即AO平分∠BAC,故②正确,
又∵AB=AC,
∴AO⊥BC,故④正确,
∵![]() ,
,
∴S△BOD=2S△AOD,
又∵△BOD≌△COE,
∴S△COE=2S△AOD,
又∵△AOD≌△AOE,
∴S△AOC=3S△AOD,
∴OC=3OD,
即![]() ,故⑤正确,
,故⑤正确,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有一Rt△ABC,∠C=90°且A(-1,3)、B(-3,-1)、C(-3,3),已知△A1AC1是由△ABC旋转得到的.若点Q在x轴上,点P在直线AB上,要使以Q、P、A1、C1为顶点的四边形是平行四边形,满足条件的点Q的坐标为______.
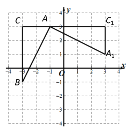
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场有一种游戏,规则是:在一只装有8个红球和若干个白球(每个球除颜色外都相同)的不透明的箱子中,随机摸出1个球,摸到红球就可获得一瓶饮料.工作人员统计了参加游戏的人数和获得饮料的人数(见下表).
(1)计算并完成表格;
参加游戏的人数
200
300
400
500
获得饮料的人数
39
63
82
99
获得饮料的频率
(2)估计获得饮料的概率;
(3)请你估计袋中白球的数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,0)和B(0,b)满足
 ,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.(1)写出A、B、C三点的坐标;
(2)当点P移动了6秒时,描出此时P点的位置,并写出点P的位置坐标;
(3)连结(2)中B、P两点,将线段BP向下平移h个单位(h>0),得到B′P′,若B′P′将四边形OACB的周长分成相等的两部分,求h的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(-4,0)、B(0,2),点P(a,a).
(1)当a=2时,将△AOB绕点P(a,a)逆时针旋转90°得△DEF,点A的对应点为D,点O的对应点为E,点B的对应点为点F,在平面直角坐标系中画出△DEF,并写出点D的坐标 ;
(2)作线段AB关于P点的中心对称图形(点A、B的对应点分别是G、H),若四边形ABGH是正方形,则a= .
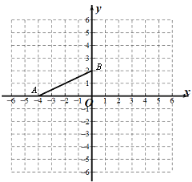
-
科目: 来源: 题型:
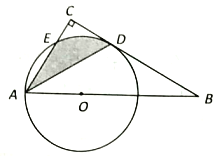
查看答案和解析>>【题目】如图,点0 为Rt△ABC斜边AB上的一点,以OA 为半径的☉O与BC切于点D,与AC 交于点E,连接AD.
(1) 求证: AD平分∠BAC;
(2)若∠BAC= 60°,OA=4,求阴影部分的面积(结果保留π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在第九章中我们研究了几种特殊四边形,请根据你的研究经验来自己研究一种特殊四边形——筝形.
初识定义:两组邻边分别相等的四边形是筝形.
(1)根据筝形的定义,写出一种你学过的四边形满足筝形的定义的是 .
性质研究:
(2)类比你学过的特殊四边形的性质,通过观察、测量、折叠、证明等操作活动,对如图的筝形ABCD(AB=AD,BC=CD)的性质进行探究,以下判断正确的有 (填序号).
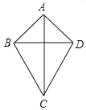
①AC⊥BD;②AC、BD互相平分;
③AC平分∠BAD和∠BCD;
④∠ABC=∠ADC;⑤∠BAD+∠BCD=180°;
⑥筝形ABCD的面积为
 AC×BD.
AC×BD.(3)在上面的筝形性质中选择一个进行证明.
性质应用:
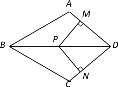
(4)直接利用你发现的筝形的性质解决下面的问题:
如图,在筝形ABCD中,AB=BC,AD=CD,点P是对角线BD上一点,过P分别做AD、CD垂线,垂足分别为点M、N.当筝形ABCD满足条件 时,四边形PNDM是正方形?请说明理由.
判定方法:
(5)回忆我们学习过的特殊四边形的判定方法(如四边相等的四边形是菱形),用文字语言写出筝形的一个判定方法(除定义外): .
相关试题

