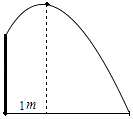
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与水池中心的水平距离为1米处达到最高,水柱落地处离池中心3米. 
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度的多少?
参考答案:
【答案】
(1)解:如图所示:以水管与地面交点为原点,原点与水柱落地点所在直线为x轴,水管所在直线为y轴,建立平面直角坐标系,
设抛物线的解析式为
:y=a(x﹣1)2+h,
代入(0,2)和(3,0)得: ![]() ,
,
解得: 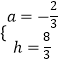 ,
,
∴抛物线的解析式为:y=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ;
;
即y=﹣ ![]() x2+
x2+ ![]() x+2(0≤x≤3)
x+2(0≤x≤3)
(2)解:y=﹣ ![]() x2+
x2+ ![]() x+2(0≤x≤3),
x+2(0≤x≤3),
当x=1时,y= ![]() ,
,
即水柱的最大高度为 ![]() m
m
【解析】(1)以水管与地面交点为原点,原点与水柱落地点所在直线为x轴,水管所在直线为y轴,建立平面直角坐标系,设抛物线的解析式为y=a(x﹣1)2+h,代入(0,2)和(3,0)得出方程组,解方程组即可,(2)求出当x=1时,y= ![]() 即可.
即可.
-
科目: 来源: 题型:
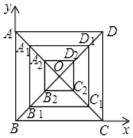
查看答案和解析>>【题目】如图以正方形ABCD的B点为坐标原点.BC所在直线为x轴,BA所在直线为y轴,建立直角坐标系.设正方形ABCD的边长为6,顺次连接OA、OB、OC、OD的中点A1、B1、C1、D1,得到正方形A1B1C1D1,再顺次连接OA1、OB1、OC1、OD1的中点得到正方形A2B2C2D2.按以上方法依次得到正方形A1B1C1D1,……AnBnCnDn,(n为不小于1的自然数),设An点的坐标为(xn,yn),则xn+yn=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
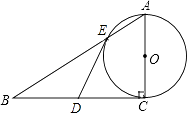
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=6,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9秒,已知∠B=30°,∠C=45°.
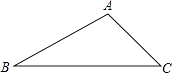
(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据: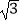 ≈1.7,
≈1.7, 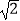 ≈1.4)
≈1.4) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD ≌ △EOC;
(2)连接AC,DE,当∠B
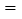 ∠AEB
∠AEB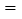 _______ °时,四边形ACED是正方形?请说明理由.
_______ °时,四边形ACED是正方形?请说明理由.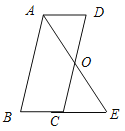
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连结CH、CG.
(1)求证:CG平分∠DCB;
(2)在正方形ABCO绕点C逆时针旋转的过程中,求线段HG、OH、BG之间的数量关系;
(3)连结BD、DA、AE、EB,在旋转的过程中,四边形AEBD是否能在点G满足一定的条件下成为矩形?若能,试求出直线DE的解析式;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
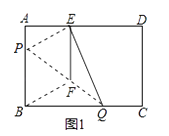
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;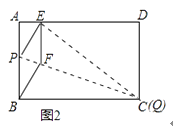
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.
相关试题

