【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.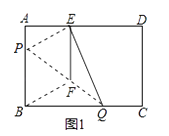
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;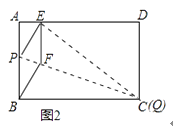
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.
参考答案:
【答案】
(1)
证明:∵折叠纸片使B点落在边AD上的E处,折痕为PQ,
∴点B与点E关于PQ对称,
∴PB=PE,BF=EF,∠BPF=∠EPF,
又∵EF∥AB,
∴∠BPF=∠EFP,
∴∠EPF=∠EFP,
∴EP=EF,
∴BP=BF=EF=EP,
∴四边形BFEP为菱形
(2)
解:①∵四边形ABCD是矩形,
∴BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°,
∵点B与点E关于PQ对称,
∴CE=BC=5cm,
在Rt△CDE中,DE= ![]() =4cm,
=4cm,
∴AE=AD﹣DE=5cm﹣4cm=1cm;
在Rt△APE中,AE=1,AP=3﹣PB=3﹣PE,
∴EP2=12+(3﹣EP)2,
解得:EP= ![]() cm,
cm,
∴菱形BFEP的边长为 ![]() cm;
cm;
②当点Q与点C重合时,如图2:
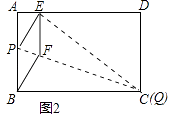
点E离点A最近,由①知,此时AE=1cm;
当点P与点A重合时,如图3所示:
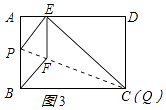
点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,
∴点E在边AD上移动的最大距离为2cm
【解析】(1)由折叠的性质得出PB=PE,BF=EF,∠BPF=∠EPF,由平行线的性质得出∠BPF=∠EFP,证出∠EPF=∠EFP,得出EP=EF,因此BP=BF=EF=EP,即可得出结论;(2)①由矩形的性质得出BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°,由对称的性质得出CE=BC=5cm,在Rt△CDE中,由勾股定理求出DE=4cm,得出AE=AD﹣DE=1cm;在Rt△APE中,由勾股定理得出方程,解方程得出EP= ![]() cm即可;②当点Q与点C重合时,点E离点A最近,由①知,此时AE=1cm;当点P与点A重合时,点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,即可得出答案.
cm即可;②当点Q与点C重合时,点E离点A最近,由①知,此时AE=1cm;当点P与点A重合时,点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与水池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.

(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度的多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD ≌ △EOC;
(2)连接AC,DE,当∠B
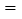 ∠AEB
∠AEB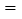 _______ °时,四边形ACED是正方形?请说明理由.
_______ °时,四边形ACED是正方形?请说明理由.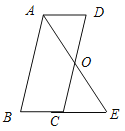
-
科目: 来源: 题型:
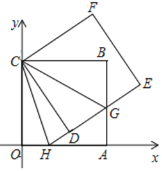
查看答案和解析>>【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连结CH、CG.
(1)求证:CG平分∠DCB;
(2)在正方形ABCO绕点C逆时针旋转的过程中,求线段HG、OH、BG之间的数量关系;
(3)连结BD、DA、AE、EB,在旋转的过程中,四边形AEBD是否能在点G满足一定的条件下成为矩形?若能,试求出直线DE的解析式;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
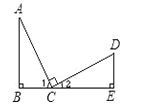
A. ∠1=∠2 B. ∠A =∠2 C. △ABC≌△CED D. ∠A与∠D互为余角
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上 A点表示的数是 a ,B 点表示的数是b ,且 ab满足|a 8|b-220.动线段 CD=4(点 D 在点 C 的右侧),从点 C与点 A重合的位置出发,以每秒 2 个单位的速度向右运动,运动时间为 t秒.
(1)求a,b的值, 运动过程中,点 D 表示的数是多少,(用含有 t 的代数式表示)
(2)在 B、C、D 三个点中,其中一个点是另外两个点为端点的线段的中点,求 t 的值;
(3)当线段 CD 在线段 AB上(不含端点重合)时,如图,图中所有线段的和记作为 S, 则 S的值是否随时间 t 的变化而变化?若变化,请说明理由;若不变,请求出 S值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
(1)在同一平面内,不相交的两条直线一定平行.(2)在同一平面内,不相交的两条线段一定平行.(3)相等的角是对顶角.(4)两条直线被第三条直线所截,同位角相等.(5)两条平行线被第三条直线所截,一对内错角的角平分线互相平行.其中,正确说法的个数是( )
A. 1个 B.2个 C.3个 D.4个
相关试题

