【题目】如图所示,梯形AOCD中,AD=9,OC=10,AO=4,在线段OC上任取一点N(不与O,C重合),连接DN,作NE⊥DN,交AO于点E.

(1)当CN=2时,求点E的坐标.
(2)若CN=x,OE=y,求y与x的函数关系式.
(3)探索与研究:若点M从O点沿OC方向、N点从C点沿CO方向同时等速运动,现有一点F,满足MF⊥MN,NF⊥ND.
①猜想F点在什么线上运动?并求出这条线所对应的函数关系式,并写出自变量的取值范围;
②求出F点在运动过程中的最高点的坐标.
参考答案:
【答案】(1)点E的坐标为(0,2);(2)①当0<x<1时,y=![]() ;②当x>1时,y=
;②当x>1时,y=![]() ;(3)①y=﹣
;(3)①y=﹣![]() x2+3x﹣
x2+3x﹣![]() (0<x<10);②最高点的坐标是(3,2).
(0<x<10);②最高点的坐标是(3,2).
【解析】试题分析:
试题解析:(1)如图所示,作DF⊥OC于F,
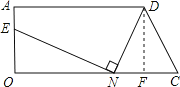
由题意知,CN=2,AD=9,OC=10.
∵AOCD是梯形且![]()
∴OF=AD=9,CF=OCOF=1,NF=CNCF=1,DF=OA=4.
∴在Rt△DFN中, ![]()
又∵NE⊥DN, ![]()
∴∠DNF=∠OEN,tan∠OEN=tan∠DNF=4.
![]()
∴点E的坐标为(0,2);
(2)如图所示:
①当0<t<1时由(1)知CF=1,所以此时N点在F点右侧,E点在y轴负半轴,
∵∠DNF=∠OEN,
![]()
整理得: ![]()
②当t>1时,如图所示N点在F点左侧,E点则在y轴正半轴,
![]()
![]()
即![]()
![]()
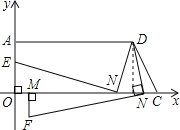
(3)①如图所示:由图知点F在第四象限,
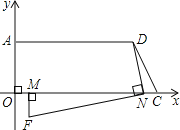
∵MF⊥MN,NF⊥ND,点F(x,y),M点、N点同时等速运动,
∴CN=
又![]()
∴∠MFN=∠DNM,
即: ![]()
y<0,
![]()
②![]()
故最高点的坐标是(3,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB上,且BE=BO,则∠EOA=___________°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】苏州太湖养殖场计划养殖蟹和贝类产品,这两个品种的种苗的总投放量只有50吨,根据经验测算,这两个品种的种苗每投放一吨的先期投资,养殖期间的投资以及产值如下表(单位:万元/吨)
品种
先期投资
养殖期间投资
产值
贝类产品
0.9
0.3
0.33
蟹产品
0.4
1
2
养殖场受经济条件的影响,先期投资不超过36万元,养殖期间的投资不超过29万元,设贝类的种苗投放量为x吨,
(1)求x的取值范围;
(2)设这两个品种产出后的总产值为y(万元),试写出y与x之间的函数关系式,并求出当x等于多少时,y有最大值?最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下表回答问题:
x
16
16.1
16.2
16.3
16.4
16.5
16.6
16.7
16.8
x2
256
259.21
262.44
265.69
268.96
272.25
175.56
278.89
282.24
(1)272.25的平方根是
(2)
 = ,
= ,  = ,
= , 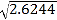 =
= (3)设
 的整数部分为a,求﹣4a的立方根.
的整数部分为a,求﹣4a的立方根. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 点为
点为 上的点,
上的点, 为
为 上的点,
上的点, ,
, ,那么
,那么 ,
,
请完成它成立的理由.
∵
 ,
, .(______)
.(______)∴
 (______)
(______)∴______
 ______,(______)
______,(______)∴
 (______)
(______)∵
 ,
,∴
 (______).
(______). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小莹用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,BC为10cm.当小莹折叠时,顶点D落在BC边上的点F处(折痕为AE).

求(1)BF的长;
(2)EF的长 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E,F为对角线BD上的两点,且∠DAE=∠BCF.
求证:(1)AE=CF;
(2)四边形AECF是平行四边形.

相关试题

