【题目】如图,小莹用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,BC为10cm.当小莹折叠时,顶点D落在BC边上的点F处(折痕为AE).

求(1)BF的长;
(2)EF的长 .
参考答案:
【答案】(1)6cm;(2)5cm
【解析】
(1)根据对折的性质,知道AF=AD=10cm,在Rt△ABF中,利用勾股定理求出BF的长;
(2)第(1)问中已求解出BF的长,从而得出FC的长,设DE=x,则EF=x,EC=8-x,在Rt△EFC中,利用勾股定理可求得x的长,从而得出EF的长.
(1)∵四边形ABCD是长方形,AB=8cm,BC=10cm,△AFE是△ADE折叠得到
∴AF=AD=BC=10cm,∠ABF=90°
∴在Rt△ABF中,BF=![]() cm
cm
(2)设DE=xcm
则FE=DE=xcm,FC=BC-BF=4cm,EC=(8-x)cm
∴在Rt△ECF中,![]()
解得:x=5
∴EF=5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下表回答问题:
x
16
16.1
16.2
16.3
16.4
16.5
16.6
16.7
16.8
x2
256
259.21
262.44
265.69
268.96
272.25
175.56
278.89
282.24
(1)272.25的平方根是
(2)
 = ,
= ,  = ,
= , 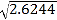 =
= (3)设
 的整数部分为a,求﹣4a的立方根.
的整数部分为a,求﹣4a的立方根. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,梯形AOCD中,AD=9,OC=10,AO=4,在线段OC上任取一点N(不与O,C重合),连接DN,作NE⊥DN,交AO于点E.

(1)当CN=2时,求点E的坐标.
(2)若CN=x,OE=y,求y与x的函数关系式.
(3)探索与研究:若点M从O点沿OC方向、N点从C点沿CO方向同时等速运动,现有一点F,满足MF⊥MN,NF⊥ND.
①猜想F点在什么线上运动?并求出这条线所对应的函数关系式,并写出自变量的取值范围;
②求出F点在运动过程中的最高点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 点为
点为 上的点,
上的点, 为
为 上的点,
上的点, ,
, ,那么
,那么 ,
,
请完成它成立的理由.
∵
 ,
, .(______)
.(______)∴
 (______)
(______)∴______
 ______,(______)
______,(______)∴
 (______)
(______)∵
 ,
,∴
 (______).
(______). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E,F为对角线BD上的两点,且∠DAE=∠BCF.
求证:(1)AE=CF;
(2)四边形AECF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AC⊥BC于C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为
 的是( )
的是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为促进课堂教学,提高教学质量,对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了如下图表,请你根据图表中提供的信息,解答下列问题.
编号
教学方式
最喜欢的频数
频率
1
教师讲,学生听
20
0.10
2
教师提出问题,学生探索思考
3
学生自行阅读教材,独立思考
30
4
分组讨论,解决问题
0.25
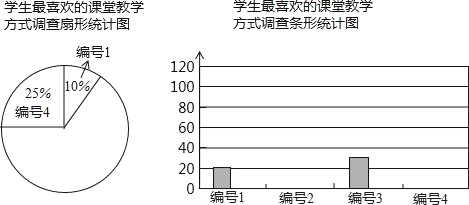
(1)收回的问卷份数为 ,把条形统计图补充完整;
(2)扇形统计图中编号1与编号4的圆心角分别是多少度?
(3)你最喜欢以上哪一种教学方式,请提出你的建议,并简要说明理由.
相关试题

