【题目】在等腰![]() 中,
中,![]() ,点
,点![]() 是直线
是直线![]() 上一点(不与
上一点(不与![]() 重合),以
重合),以![]() 为一边在
为一边在![]() 的右侧作等腰
的右侧作等腰![]() ,使
,使![]() ,
,![]() ,连结
,连结![]() .
.
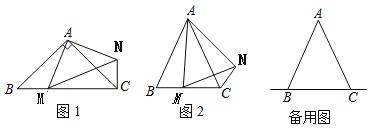
(1)如图1,当点![]() 在线段
在线段![]() 上时,如果
上时,如果![]() ,则
,则![]() _______°.
_______°.
(2)设![]() .
.
①如图2,当点![]() 在线段
在线段![]() 上移动时,
上移动时,![]() 之间有怎样的数量关系?请说明理由.
之间有怎样的数量关系?请说明理由.
②当点![]() 在直线
在直线![]() 上移动时,
上移动时,![]() 之间有怎样的数量关系?请你直接写出你的结论.
之间有怎样的数量关系?请你直接写出你的结论.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() 之间的数量关系是
之间的数量关系是![]() ,理由见解析;②结论:
,理由见解析;②结论: ![]() ,
,![]() .
.
【解析】
(1)先用等式的性质得出∠CAN=∠BAM,进而得出△ABM≌△ACN,有∠B=∠ACE,最后用等式的性质即可得出结论
(2)①由(1)的结论即可得出α+β=180°;②同(1)的方法即可得出结论.
(1)![]() ,
,![]()
![]()
在△ABM和△ACN中
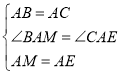
![]()
![]()
![]()
∴![]()
(2)①解:![]() 之间的数量关系是
之间的数量关系是![]()
理由:
![]() (已知)
(已知)
![]() (等式性质)
(等式性质)
即![]()
在![]() 和
和![]() 中
中
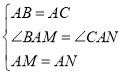
![]()
![]() (全等三角形对应角相等)
(全等三角形对应角相等)
![]() (三角形的内角和为180°)
(三角形的内角和为180°)
![]() (等量代换)
(等量代换)
![]()
![]() (等量代换)
(等量代换)
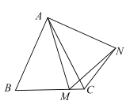
②结论:
1)当点![]() (不与
(不与![]() 重合)在射线
重合)在射线![]() 上时,
上时,
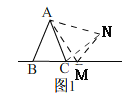
同(1)的方法可得![]()
![]() ,
,
![]()
![]()
![]() 之间的数量关系是
之间的数量关系是![]()
2)当点![]() (不与
(不与![]() 重合)在射线
重合)在射线![]() 的反向延长线上时,
的反向延长线上时,

同(1)的方法可得![]()
![]() ,
,
![]()
![]()
![]() 之间的数量关系是
之间的数量关系是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面内,已知点
 的坐标是
的坐标是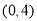 ,点
,点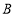 的坐标是
的坐标是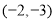
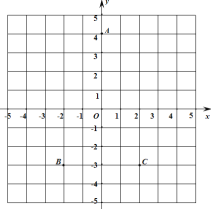
(1)图中点
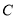 的坐标是_______.
的坐标是_______.(2)点
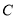 关于
关于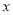 轴对称的点
轴对称的点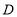 的坐标是_______.
的坐标是_______.(3)如果将点
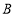 沿着与
沿着与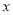 轴平行的方向向右平移2个单位得到点
轴平行的方向向右平移2个单位得到点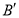 ,那么
,那么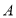 、
、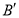 两点之间的距离是__.
两点之间的距离是__.(4)图中
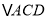 的面积是______.
的面积是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,∠ABC=∠ADC.试判断AC与BD的位置关系,并说明理由.

-
科目: 来源: 题型:
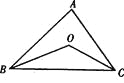
查看答案和解析>>【题目】如图,在△ ABC中,∠ ABC、∠ ACB的平分线交于点O。
(1)若∠ABC=40°,∠ ACB=50°,则∠BOC=_______
(2)若∠ABC+∠ ACB=lO0°,则∠BOC="________"
(3)若∠A=70°,则∠BOC=_________
(4)若∠BOC=140°,则∠A=________
(5)你能发现∠ BOC与∠ A之间有什么数量关系吗?写出并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.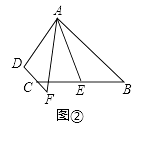
(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.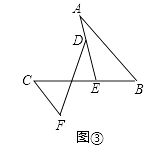
-
科目: 来源: 题型:
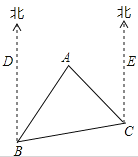
查看答案和解析>>【题目】如图,A岛在B岛的北偏东30°方向,C岛在B岛的北偏东80°方向,A岛在C岛北偏西40°方向.从A岛看B、C两岛的视角∠BAC是多少?
相关试题

