【题目】如图,已知AB=AD,∠ABC=∠ADC.试判断AC与BD的位置关系,并说明理由.

参考答案:
【答案】AC⊥BD,理由见解析.
【解析】
AC与BD垂直,理由为:由AB=AD,利用等边对等角得到一对角相等,利用等式性质得到∠BDC=∠DBC,利用等角对等边得到DC=BC,利用SSS得到三角形ABC与三角形ADC全等,利用全等三角形对应角相等得到∠DAC=∠BAC,再利用三线合一即可得证.
AC⊥BD,理由为:
∵AB=AD(已知),
∴∠ADB=∠ABD(等边对等角),
∵∠ABC=∠ADC(已知),
∴∠ABC﹣∠ABD=∠ADC﹣∠ADB(等式性质),
即∠BDC=∠DBC,
∴DC=BC(等角对等边),
在△ABC和△ADC中,
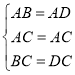
∴△ABC≌△ADC(SSS),
∴∠DAC=∠BAC(全等三角形的对应角相等),
又∵AB=AD,
∴AC⊥BD(等腰三角形三线合一).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
(1)当抛物线经过点(﹣2,0)和(﹣1,3)时,求抛物线的表达式;
(2)当抛物线的顶点在直线y=﹣2x上时,求b的值;
(3)如图,现有一组这样的抛物线,它们的顶点A1、A2、…,An在直线y=﹣2x上,横坐标依次为﹣1,﹣2,﹣3,…,﹣n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1、B2 , …,Bn , 以线段AnBn为边向左作正方形AnBnCnDn , 如果这组抛物线中的某一条经过点Dn , 求此时满足条件的正方形AnBnCnDn的边长.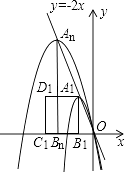
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面内,已知点
 的坐标是
的坐标是 ,点
,点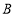 的坐标是
的坐标是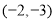
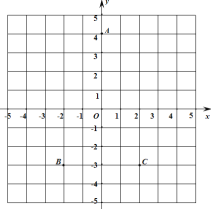
(1)图中点
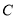 的坐标是_______.
的坐标是_______.(2)点
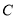 关于
关于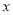 轴对称的点
轴对称的点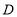 的坐标是_______.
的坐标是_______.(3)如果将点
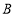 沿着与
沿着与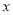 轴平行的方向向右平移2个单位得到点
轴平行的方向向右平移2个单位得到点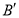 ,那么
,那么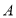 、
、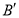 两点之间的距离是__.
两点之间的距离是__.(4)图中
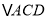 的面积是______.
的面积是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰
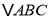 中,
中,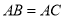 ,点
,点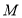 是直线
是直线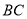 上一点(不与
上一点(不与 重合),以
重合),以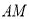 为一边在
为一边在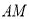 的右侧作等腰
的右侧作等腰 ,使
,使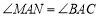 ,
, ,连结
,连结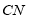 .
.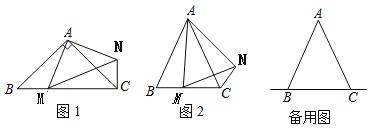
(1)如图1,当点
 在线段
在线段 上时,如果
上时,如果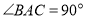 ,则
,则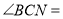 _______°.
_______°.(2)设
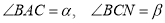 .
.①如图2,当点
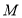 在线段
在线段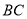 上移动时,
上移动时,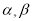 之间有怎样的数量关系?请说明理由.
之间有怎样的数量关系?请说明理由.②当点
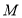 在直线
在直线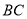 上移动时,
上移动时,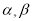 之间有怎样的数量关系?请你直接写出你的结论.
之间有怎样的数量关系?请你直接写出你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ ABC中,∠ ABC、∠ ACB的平分线交于点O。
(1)若∠ABC=40°,∠ ACB=50°,则∠BOC=_______
(2)若∠ABC+∠ ACB=lO0°,则∠BOC="________"
(3)若∠A=70°,则∠BOC=_________
(4)若∠BOC=140°,则∠A=________
(5)你能发现∠ BOC与∠ A之间有什么数量关系吗?写出并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
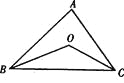
(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.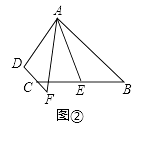
(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.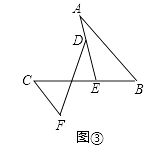
相关试题

