搜索
【题目】计算
（1）9+（﹣7）+10+（﹣3）+（﹣9）
（2）12+（﹣14）+6+（﹣7）
（3）﹣ 
（4）﹣4.2+5.7+（﹣8.7）+4.2．
参考答案：
【答案】（1）0；（2）﹣3；（3）﹣1 
；（4）﹣3 .
【解析】
（1）首先写成省略括号的形式，然后再找相反数，再计算即可；
（2）首先写成省略括号的形式，然后再同号两数相加，再异号两数相加进行计算即可；
（3）首先写成省略括号的形式，然后再同分母的两数相加，再进一步进行计算即可；
（4）首先写成省略括号的形式，然后再找相反数，再计算即可．
（1）原式=9﹣7+10﹣3﹣9=0
（2）原式=12﹣14+6﹣7=﹣3
（3）原式=﹣
﹣
﹣
+
=﹣1﹣=﹣1
（4）原式=﹣4.2+4.2+5.7﹣8.7=﹣3
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图∠1=∠2，CF⊥AB，DE⊥AB，求证：FG∥BC.
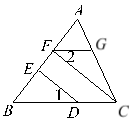
证明：∵CF⊥AB，DE⊥AB （已知）
∴∠BED=90°，∠BFC=90°（ ）
∴∠BED=∠BFC （ ）
∴ED∥FC （ ）
∴∠1=∠BCF （ ）
∵∠2=∠1 （ 已知 ）
∴∠2=∠BCF （ ）
∴FG∥BC （ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，E是△ABC中BC边上的一点，且BE=
BC；点D是AC上一点，且AD= 
AC，S△ABC=24，则S△BEF﹣S△ADF=（ ） 
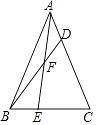
A.1
B.2
C.3
D.4 -
科目： 来源： 题型：
查看答案和解析>>【题目】小刚在课外书中看到这样一道有理数的混合运算题：
计算：
她发现，这个算式反映的是前后两部分的和，而这两部分之间存在着某种关系，利用这种关系，他顺利地解答了这道题。
（1）前后两部分之间存在着什么关系？
（2）先计算哪步分比较简便？并请计算比较简便的那部分。
（3）利用（1）中的关系，直接写出另一部分的结果。
（4）根据以上分析，求出原式的结果。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知矩形ABCD中，E是AD上的一点，F是AB上的一点，EF⊥EC，且EF=EC，DE=4cm，矩形ABCD的周长为32cm，求AE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图（1）所示，E为矩形ABCD的边AD上一点，动点P，Q同时从点B出发，点P沿折线BE﹣ED﹣DC运动到点C时停止，点Q沿BC运动到点C时停止，它们运动的速度都是1cm/秒．设P、Q同时出发t秒时，△BPQ的面积为ycm2 ． 已知y与t的函数关系图象如图（2）（曲线OM为抛物线的一部分），则下列结论：①AD=BE=5；②
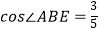；③当0＜t≤5时， 
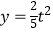；④当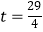 
秒时，△ABE∽△QBP；其中正确的结论是（ ）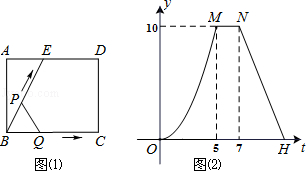
A.①②③
B.②③
C.①③④
D.②④ -
科目： 来源： 题型：
查看答案和解析>>【题目】（1）在如图所示的数轴上，把数﹣2，
，4，﹣
，2.5表示出来，并用“＜“将它们连接起来；（2）假如在原点处放立一挡板（厚度不计），有甲、乙两个小球（忽略球的大小，可看作一点），小球甲从表示数﹣2的点处出发，以1个单位长度/秒的速度沿数轴向左运动；同时小球乙从表示数4的点处出发，以2个单位长度/秒的速度沿数轴向左运动，在碰到挡板后即刻按原来的速度向相反的方向运动，设运动的时间为t（秒）．
请从A，B两题中任选一题作答．
A．当t=3时，求甲、乙两小球之间的距离．
B．用含t的代数式表示甲、乙两小球之间的距离．
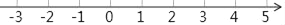
相关试题
