【题目】如图,在△ABC中,已知∠BDC=∠EFD,∠AED=∠ACB.
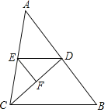
(1)试判断∠DEF与∠B的大小关系,并说明理由;
(2)若D、E、F分别是AB、AC、CD边上的中点,S△DEF=4,S△ABC=
参考答案:
【答案】(1)∠DEF=∠B,理由见解析;(2)32
【解析】
(1)延长EF交BC于G,根据平行四边形的判定和性质即可得到结论;
(2)根据三角形一边的中线平分三角形的面积,即可得到结论.
(1)∠DEF=∠B,理由如下:
延长EF交BC于G,
∵∠BDC=∠EFD,
∴EF∥BD,
∵∠AED=∠ACB,
∴DE∥BC,
∴四边形DEGB是平行四边形,
∴∠DEF=∠B;
(2)∵F是CD边上的中点,S△DEF=4,
∴S△DEC=2S△DEF=8,
∵E是AC边上的中点,
∴S△ADC=2S△DEC=16,
∵D是AB边上的中点,
∴S△ABC=2S△ACD=32.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,BD为∠ABC的角平分线,DE、DF分别是∠ADB和∠ADC的角平分线,且∠BDF=α,则∠A与∠C的等量关系是________________(等式中含有α)

-
科目: 来源: 题型:
查看答案和解析>>【题目】小丹、小林是某中学八年级的同班同学,在升入九年级时,学校打算重新组班,他们将被随机编入A,B,C三个班.
(1)请你用画树状图法或列表法,列出所有可能的结果;
(2)求两人再次成为同班同学的概率. -
科目: 来源: 题型:
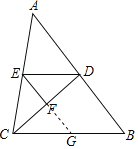
查看答案和解析>>【题目】在如图所示的方格纸中,小正方形的顶点叫做格点,△ABC是一个格点三角形(即△ABC的三个顶点都在格点上),根据要求回答下列问题:

(1)画出△ABC先向左平移6格,再向上平移1格所得的△A′B′C′;
(2)利用网格画出△ABC中BC边上的高AD.
(3)过点A画直线l,将△ABC分成面积相等的两个三角形;
(4)在直线AB的右侧格点图中标出所有格点E(不包括点C),使S△ABE=S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接济川中学红歌演讲比赛,济川校区七年级(15)(16)班决定订购同一套服装,两班一共有103人(15班人数多于16班),经协商,某服装店给出的价格如下:
购买人数/人
1~50人
50~100人
100以上人
每套服装价格/元
50
45
40
例如:若购买人数为60人,则购买共需花费60×45=2700元.
(1)如果两个班都以班为单位分别购买,则一共需花费4875元,那么15,16班各有多少名学生?
(2)如果两个班联合起来,做为一个整体购买,则能节省多少元钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
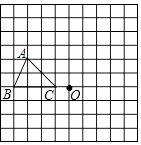
(1)画出△ABC绕点O顺时针旋转90°后的△A1B1C1;
(2)求△OAA1的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】图为放置在水平桌面上的台灯的平面示意图,可伸缩式灯臂AO长为40cm,与水平面所形成的夹角∠OAM恒为75°(不受灯臂伸缩的影响),由光源O射出的光线沿灯罩形成光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,

(1)求该台灯照亮桌面的宽度BC(不考虑其他因素,结果精确到1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,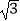 ≈1.73)
≈1.73)
(2)若灯臂最长可伸长至60cm,不调整灯罩的角度,能否让台灯照亮桌面85cm的宽度?
相关试题

