【题目】如图,在Rt△ABC中,AB=BC,∠ABC=90°,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF,给出以下五个结论: ① ![]() ;②∠ADF=∠CDB;③点F是GE的中点;④AF=
;②∠ADF=∠CDB;③点F是GE的中点;④AF= ![]() AB;⑤S△ABC=5S△BDF ,
AB;⑤S△ABC=5S△BDF ,
其中正确结论的序号是 . 
参考答案:
【答案】①②④
【解析】解:依题意可得BC∥AG, ∴△AFG∽△BFC,∴ ![]() ,
,
又AB=BC,∴ ![]() .
.
故结论①正确;
如右图,∵∠1+∠3=90°,∠1+∠4=90°,∴∠3=∠4.
在△ABG与△BCD中,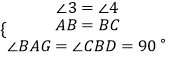 ,
,
∴△ABG≌△BCD(ASA),
∴AG=BD,又BD=AD,∴AG=AD;
在△AFG与△AFD中,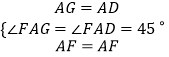 ,
,
∴△AFG≌△AFD(SAS),∴∠5=∠2,
又∠5+∠3=∠1+∠3=90°,∴∠5=∠1,
∴∠1=∠2,即∠ADF=∠CDB.
故结论②正确;
∵△AFG≌△AFD,∴FG=FD,又△FDE为直角三角形,∴FD>FE,
∴FG>FE,即点F不是线段GE的中点.
故结论③错误;
∵△ABC为等腰直角三角形,∴AC= ![]() AB;
AB;
∵△AFG≌△AFD,∴AG=AD= ![]() AB=
AB= ![]() BC;
BC;
∵△AFG∽△BFC,∴ ![]() ,∴FC=2AF,
,∴FC=2AF,
∴AF= ![]() AC=
AC= ![]() AB.
AB.
故结论④正确;
∵AF= ![]() AC,∴S△ABF=
AC,∴S△ABF= ![]() S△ABC;又D为中点,∴S△BDF=
S△ABC;又D为中点,∴S△BDF= ![]() S△ABF ,
S△ABF ,
∴S△BDF= ![]() S△ABC , 即S△ABC=6S△BDF .
S△ABC , 即S△ABC=6S△BDF .
故结论⑤错误.
综上所述,结论①②④正确,
所以答案是:①②④.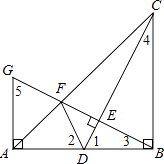
【考点精析】根据题目的已知条件,利用等腰直角三角形和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P是不等边△ABC的边BC上的一点,点D在边AB或AC上,若由点P、D截得的小三角形与△ABC相似,那么D点的位置最多有( )

A.2处
B.3处
C.4处
D.5处 -
科目: 来源: 题型:
查看答案和解析>>【题目】请你用学习“一次函数”时积累的经验和方法解决下列问题:
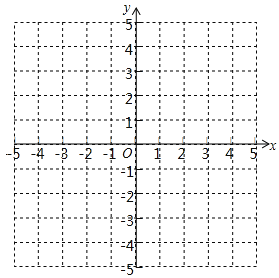
(1)在平面直角坐标系中,画出函数y=|x|的图象;
①列表填空:
x
…
-3
-2
-1
0
1
2
3
…
y
…
…
②描点、连线,在图所示的平面直角坐标系中画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|的两条不同类型的性质.
-
科目: 来源: 题型:
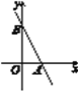
查看答案和解析>>【题目】如图,已知直线y=-2x+6与x轴交于点A,与y轴交于点B.
(1)点A的坐标为________,点B的坐标为________.
(2)求△AOB的面积.
(3)直线AB上是否存在一点C(点C与点B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题。
(1)用适当的方法解下列一元二次方程:x2﹣6x+1=0.
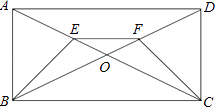
(2)如图,已知E、F分别是矩形ABCD的对角线AC和BD上的点,且AE=DF,求证:BE=CF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( )

A.2010年至2014年间工业生产总值逐年增加
B.2014年的工业生产总值比前一年增加了40亿元
C.2012年与2013年每一年与前一年比,其增长额相同
D.从2011年至2014年,每一年与前一年比,2014年的增长率最大
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(k﹣1)x2﹣(k﹣1)x+
 =0有两个相等的实数根,求k的值.
=0有两个相等的实数根,求k的值.
相关试题

