【题目】计算题。 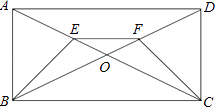
(1)用适当的方法解下列一元二次方程:x2﹣6x+1=0.
(2)如图,已知E、F分别是矩形ABCD的对角线AC和BD上的点,且AE=DF,求证:BE=CF.
参考答案:
【答案】
(1)解:x2﹣6x+1=0.
移项得,x2﹣6x=﹣1,
配方得,x2﹣6x+9=﹣1+9,
∴(x﹣3)2=8,
∴x﹣3=±2 ![]() ,
,
∴x1=3+2 ![]() ,x2=3﹣2
,x2=3﹣2 ![]()
(2)证明:∵矩形ABCD的对角线为AC和BD,
∴AO=CO=BO=DO,
∵E、F分别是矩形ABCD的对角线AC和BD上的点,AE=DF,
∴EO=FO,
在△BOE和△COF中, 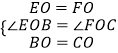 ,
,
∴△BOE≌△COF(SAS),
∴BE=CF.
【解析】(1)用配方法解一元二次方程,首先将常数项移到等号的右侧,将等号左右两边同时加上一次项系数一半的平方,即可将等号左边的代数式写成完全平方形式.(2)根据矩形对角线的性质,矩形对角线互相平分且相等,可知EO=FO,BO=CO,∠BOE=∠COF,可知△BOE≌△COF,即可得出BE=CF.
【考点精析】利用矩形的性质对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你用学习“一次函数”时积累的经验和方法解决下列问题:
(1)在平面直角坐标系中,画出函数y=|x|的图象;
①列表填空:
x
…
-3
-2
-1
0
1
2
3
…
y
…
…
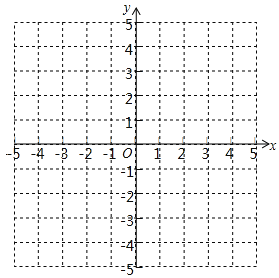
②描点、连线,在图所示的平面直角坐标系中画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|的两条不同类型的性质.
-
科目: 来源: 题型:
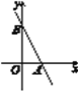
查看答案和解析>>【题目】如图,已知直线y=-2x+6与x轴交于点A,与y轴交于点B.
(1)点A的坐标为________,点B的坐标为________.
(2)求△AOB的面积.
(3)直线AB上是否存在一点C(点C与点B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
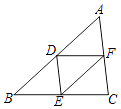
查看答案和解析>>【题目】如图,在Rt△ABC中,AB=BC,∠ABC=90°,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF,给出以下五个结论: ①
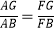 ;②∠ADF=∠CDB;③点F是GE的中点;④AF=
;②∠ADF=∠CDB;③点F是GE的中点;④AF= 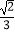 AB;⑤S△ABC=5S△BDF ,
AB;⑤S△ABC=5S△BDF ,
其中正确结论的序号是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( )

A.2010年至2014年间工业生产总值逐年增加
B.2014年的工业生产总值比前一年增加了40亿元
C.2012年与2013年每一年与前一年比,其增长额相同
D.从2011年至2014年,每一年与前一年比,2014年的增长率最大
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(k﹣1)x2﹣(k﹣1)x+
 =0有两个相等的实数根,求k的值.
=0有两个相等的实数根,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D、E、F分别为△ABC的三边中点,试说明△ABC∽△EFD.
相关试题

