【题目】如图,![]() 是一条射线,
是一条射线,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的平分线.
的平分线.
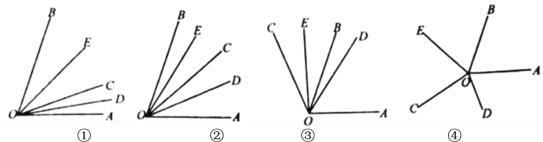
(1)如图①,当![]() 时,则
时,则![]() 的度数为________________;
的度数为________________;
(2)如图②,当射线![]() 在
在![]() 内绕
内绕![]() 点旋转时,
点旋转时,![]() 、
、![]() 、
、![]() 三角之间有怎样的数量关系?并说明理由;
三角之间有怎样的数量关系?并说明理由;
(3)当射线![]() 在
在![]() 外如图③所示位置时,(2)中三个角:
外如图③所示位置时,(2)中三个角:![]() 、
、![]() 、
、![]() 之间数量关系的结论是否还成立?给出结论并说明理由;
之间数量关系的结论是否还成立?给出结论并说明理由;
(4)当射线![]() 在
在![]() 外如图④所示位置时,
外如图④所示位置时,![]() 、
、![]() 、
、![]() 之间数量关系是____________.
之间数量关系是____________.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,详见解析;(3)不成立,
,详见解析;(3)不成立,![]() ,详见解析;(4)
,详见解析;(4)![]() ;
;
【解析】
(1)(2)根据角平分线定义得出∠DOC=![]() ∠AOC,∠EOC=
∠AOC,∠EOC=![]() ∠BOC,求出∠DOE=
∠BOC,求出∠DOE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() AOB,即可得出答案;(3)根据角平分线定义得出∠DOC=
AOB,即可得出答案;(3)根据角平分线定义得出∠DOC=![]() ∠AOC,∠EOC=
∠AOC,∠EOC=![]() ∠BOC,求出∠DOE=
∠BOC,求出∠DOE=![]() (∠AOC∠BOC)=
(∠AOC∠BOC)=![]() ∠AOB,即可得出答案;(4)根据角平分线定义即可求解.
∠AOB,即可得出答案;(4)根据角平分线定义即可求解.
解:当射线OC在∠AOB的内部时,
∵OD,OE分别为∠AOC,∠BOC的角平分线,
∴∠DOC=![]() ∠AOC,∠EOC=
∠AOC,∠EOC=![]() ∠BOC,
∠BOC,
∴∠DOE=∠DOC+∠EOC=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB,
∠AOB,
(1)若∠AOB=80°,则∠DOE的度数为40°.
故答案为:40;
(2)∠DOE=∠DOC+∠EOC=![]() ∠AOC+
∠AOC+![]() ∠BOC=∠BOE+∠DOA.
∠BOC=∠BOE+∠DOA.
(3)当射线OC在∠AOB的外部时 (1)中的结论不成立.理由是:
∵OD、OE分别是∠AOC、∠BOC的角平分线
∴∠COD=![]() ∠AOC,
∠AOC,
∠EOC=![]() ∠BOC,
∠BOC,
∠DOE=∠COD∠EOC![]() ∠AOC
∠AOC![]() ∠BOC=∠AOD∠BOE.
∠BOC=∠AOD∠BOE.
(4)∵OD,OE分别为∠AOC,∠BOC的角平分线,
∴∠DOC=∠AOD,∠EOC=∠BOE,
∴∠DOE=∠DOC+∠EOC=∠BOE+∠DOA.
故∠BOE、∠EOD、∠DOA之间数量关系是∠DOE=∠BOE+∠DOA.
故答案为:∠DOE=∠BOE+∠DOA.
-
科目: 来源: 题型:
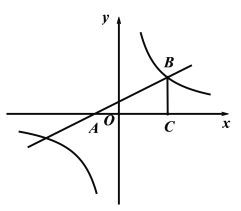
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,直线
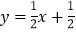 与x轴交于点A,在第一象限内与反比例函数图像交于点B,BC垂直于x轴,垂足为点C,且OC=2AO.求
与x轴交于点A,在第一象限内与反比例函数图像交于点B,BC垂直于x轴,垂足为点C,且OC=2AO.求(1)点
 的坐标;
的坐标;(2)反比例函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的
 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这
 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
-
科目: 来源: 题型:
查看答案和解析>>【题目】兴隆商场用36万元购进A、B两种品牌的服装,销售完后共获利6万元,其进价和售价如下表:
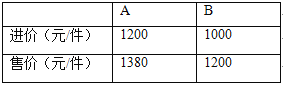
该商场购进A、B两种服装各多少件?
(2)第二次以原价购进A、B两种服装,购进B服装的件数不变,购进A服装的件数是第一次的2倍,A种服装按原价出售,而B种服装打折销售;若两种服装销售完毕,要使第二次销售活动获利不少于81600元,则B种服装最低打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线
 上有三点
上有三点 、
、 、
、 ,满足
,满足 ,
, ,
, ,点
,点 从点
从点 出发,沿
出发,沿 方向以
方向以 的速度匀速运动,点
的速度匀速运动,点 从点
从点 出发在线段
出发在线段 上向点
上向点 匀速运动,两点同时出发,当点
匀速运动,两点同时出发,当点 运动到点
运动到点 时,点
时,点 、
、 停止运动.
停止运动.

(1)若点
 运动速度为
运动速度为 ,经过多长时间
,经过多长时间 、
、 两点相遇?
两点相遇?(2)当
 时,点
时,点 运动到的位置恰好是线段
运动到的位置恰好是线段 的中点,求点
的中点,求点 的运动速度;
的运动速度;(3)设运动时间为
 ,当点
,当点 运动到线段
运动到线段 上时,分别取
上时,分别取 和
和 的中点
的中点 、
、 ,则
,则 ____________
____________ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于D,连结DC、DA、OA、OC,四边形OADC为平行四边形.
(1)求证:△BOC≌△CDA.
(2)若AB=2,求阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的一元二次方程:(m﹣1)x2+(m﹣2)x﹣1=0(m为实数).
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)若
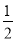 是此方程的实数根,抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B,抛物线的顶点为C,求△ABC的面积.
是此方程的实数根,抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B,抛物线的顶点为C,求△ABC的面积.
相关试题

