【题目】如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于D,连结DC、DA、OA、OC,四边形OADC为平行四边形.
(1)求证:△BOC≌△CDA.
(2)若AB=2,求阴影部分的面积.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析: (1)根据内心性质得∠1=∠2,∠3=∠4,则AD=CD,于是可判断四边形OADC为菱形,则BD垂直平分AC,∠4=∠5=∠6,易得OA=OC,∠2=∠3,所以OB=OC,可判断点O为△ABC的外心,则可判断△ABC为等边三角形,所以∠AOB=∠BOC=∠AOC=120°,BC=AC,再根据平行四边形的性质得∠ADC=∠AOC=120°,AD=OC,CD=OA=OB,则根据“SAS”证明△BOC≌△CDA;
(2)作OH⊥AB于H,如图,根据等腰三角形的性质和三角形内角和定理得到∠BOH=30°,根据垂径定理得到BH=AH=![]() AB=1,再利用含30度的直角三角形三边的关系得到OH=
AB=1,再利用含30度的直角三角形三边的关系得到OH=![]() BH=
BH=![]() ,OB=2OH=
,OB=2OH=![]() ,然后根据三角形面积公式和扇形面积公式,利用S阴影部分=S扇形AOB-S△AOB进行计算即可.
,然后根据三角形面积公式和扇形面积公式,利用S阴影部分=S扇形AOB-S△AOB进行计算即可.
详解:
(1)证明:∵O是△ABC的内心,

∴∠2=∠3,∠5=∠6,
∵∠1=∠2,∴∠1=∠3,
由AD∥CO,AD=CO,∴∠4=∠6,
∴△BOC≌△CDA(AAS)
(2)由(1)得,BC=AC,∠3=∠4=∠6,
∴∠ABC=∠ACB
∴AB=AC
∴△ABC是等边三角形
∴O是△ABC的内心也是外心
∴OA=OB=OC
设E为BD与AC的交点,BE垂直平分AC.
在Rt△OCE中,CE=![]() AC=
AC=![]() AB=1,∠OCE=30°,
AB=1,∠OCE=30°,
∴OA=OB=OC=![]()
∵∠AOC=120°,
∴![]()
=![]()
=![]()
点睛: 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了等边三角形的判定与性质和扇形面积的计算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】兴隆商场用36万元购进A、B两种品牌的服装,销售完后共获利6万元,其进价和售价如下表:
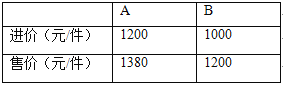
该商场购进A、B两种服装各多少件?
(2)第二次以原价购进A、B两种服装,购进B服装的件数不变,购进A服装的件数是第一次的2倍,A种服装按原价出售,而B种服装打折销售;若两种服装销售完毕,要使第二次销售活动获利不少于81600元,则B种服装最低打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
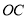 是一条射线,
是一条射线,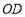 、
、 分别是
分别是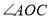 和
和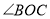 的平分线.
的平分线.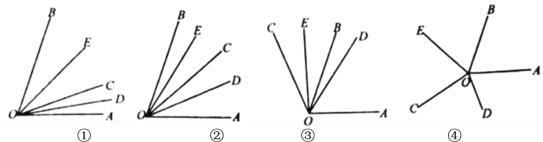
(1)如图①,当
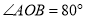 时,则
时,则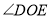 的度数为________________;
的度数为________________;(2)如图②,当射线
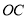 在
在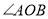 内绕
内绕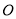 点旋转时,
点旋转时,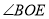 、
、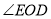 、
、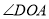 三角之间有怎样的数量关系?并说明理由;
三角之间有怎样的数量关系?并说明理由;(3)当射线
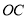 在
在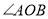 外如图③所示位置时,(2)中三个角:
外如图③所示位置时,(2)中三个角: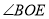 、
、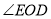 、
、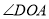 之间数量关系的结论是否还成立?给出结论并说明理由;
之间数量关系的结论是否还成立?给出结论并说明理由;(4)当射线
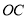 在
在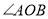 外如图④所示位置时,
外如图④所示位置时,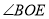 、
、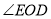 、
、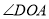 之间数量关系是____________.
之间数量关系是____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线
 上有三点
上有三点 、
、 、
、 ,满足
,满足 ,
, ,
, ,点
,点 从点
从点 出发,沿
出发,沿 方向以
方向以 的速度匀速运动,点
的速度匀速运动,点 从点
从点 出发在线段
出发在线段 上向点
上向点 匀速运动,两点同时出发,当点
匀速运动,两点同时出发,当点 运动到点
运动到点 时,点
时,点 、
、 停止运动.
停止运动.

(1)若点
 运动速度为
运动速度为 ,经过多长时间
,经过多长时间 、
、 两点相遇?
两点相遇?(2)当
 时,点
时,点 运动到的位置恰好是线段
运动到的位置恰好是线段 的中点,求点
的中点,求点 的运动速度;
的运动速度;(3)设运动时间为
 ,当点
,当点 运动到线段
运动到线段 上时,分别取
上时,分别取 和
和 的中点
的中点 、
、 ,则
,则 ____________
____________ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的一元二次方程:(m﹣1)x2+(m﹣2)x﹣1=0(m为实数).
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)若
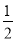 是此方程的实数根,抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B,抛物线的顶点为C,求△ABC的面积.
是此方程的实数根,抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B,抛物线的顶点为C,求△ABC的面积. -
科目: 来源: 题型:
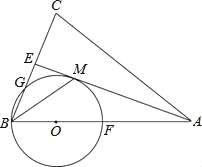
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中,点
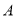 、
、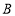 、
、 是三个格点(网格线的交点叫做格点)
是三个格点(网格线的交点叫做格点)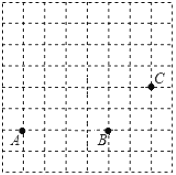
(1)画线段
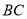 ,画射线
,画射线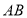 ,过点
,过点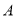 画
画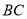 的平行线
的平行线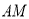 ;
;(2)过点
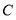 画直线
画直线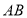 的垂线,垂足为点
的垂线,垂足为点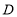 ,则点
,则点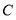 到
到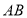 的距离是线段______的长度;
的距离是线段______的长度;(3)线段
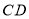 ______线段
______线段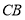 (填“>”或“<”),理由是______.
(填“>”或“<”),理由是______.
相关试题

