Question

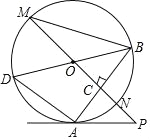
【题目】如图，已知⊙O中，AB为弦，直线PO交⊙O于点M、N，PO⊥AB于C，过点B作直径BD，连接AD、BM、AP．

（1）求证：PM∥AD；

（2）若∠BAP=2∠M，求证：PA是⊙O的切线；

（3）若AD=6，tan∠M=，求⊙O的直径．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）5；

【解析】

（1）根据平行线的判定求出即可；（2）连接OA，求出∠OAP=∠BAP+∠OAB=∠BOC+∠OBC=90°，根据切线的判定得出即可；（3）设BC=x，CM=2x，根据相似三角形的性质和判定求出NC=x，求出MN=2x+x=2.5x，OM=MN=1.25x，OC=0.75x，根据三角形的中位线性质得出0.75x=AD=3，求出x即可．

（1）∵BD是直径，

∴∠DAB=90°，

∵PO⊥AB，

∴∠DAB=∠MCB=90°，

∴PM∥AD；

（2）连接OA，

∵OB=OM，

∴∠M=∠OBM，

∴∠BON=2∠M，

∵∠BAP=2∠M，

∴∠BON=∠BAP，

∵PO⊥AB，

∴∠ACO=90°，

∴∠AON+∠OAC=90°，

∵OA=OB，

∴∠BON=∠AON，

∴∠BAP=∠AON，

∴∠BAP+∠OAC=90°，

∴∠OAP=90°，

∵OA是半径，

∴PA是⊙O的切线；

（3）连接BN，

则∠MBN=90°．

∵tan∠M=，

∴=，

设BC=x，CM=2x，

∵MN是⊙O直径，NM⊥AB，

∴∠MBN=∠BCN=∠BCM=90°，

∴∠NBC=∠M=90°﹣∠BNC，

∴△MBC∽△BNC，

∴，

∴BC2=NC×MC，

∴NC=x，

∴MN=2x+x=2.5x，

∴OM=MN=1.25x，

∴OC=2x﹣1.25x=0.75x，

∵O是BD的中点，C是AB的中点，AD=6，

∴OC=0.75x=AD=3，

解得：x=4，

∴MO=1.25x=1.25×4=5，

∴⊙O的半径为5．