【题目】如图,在平面直角坐标系中,等边三角形ABC的顶点B与原点O重合,点C在x轴上,点C坐标为(6,0),等边三角形ABC的三边上有三个动点D、E、F(不考虑与A、B、C重合),点D从A向B运动,点E从B向C运动,点F从C向A运动,三点同时运动,到终点结束,且速度均为1cm/s,设运动的时间为ts,解答下列问题:
(1)求证:如图①,不论t如何变化,△DEF始终为等边三角形.
(2)如图②过点E作EQ∥AB,交AC于点Q,设△AEQ的面积为S,求S与t的函数关系式及t为何值时△AEQ的面积最大?求出这个最大值.
(3)在(2)的条件下,当△AEQ的面积最大时,平面内是否存在一点P,使A、D、Q、P构成的四边形是菱形,若存在请直接写出P坐标,若不存在请说明理由?

参考答案:
【答案】(1)证明见解析;(2)当t=3时,△AEQ的面积最大为![]() cm2;(3)(3,0)或(6,3
cm2;(3)(3,0)或(6,3![]() )或(0,3
)或(0,3![]() )
)
【解析】
(1)由三角形ABC为等边三角形,以及AD=BE=CF,进而得出三角形ADF与三角形CFE与三角形BED全等,利用全等三角形对应边相等得到BF=DF=DE,即可得证;(2)先表示出三角形AEC面积,根据EQ与AB平行,得到三角形CEQ与三角形ABC相似,利用相似三角形面积比等于相似比的平方表示出三角形CEQ面积,进而表示出AEQ面积,利用二次函数的性质求出面积最大值,并求出此时Q的坐标即可;(3)当△AEQ的面积最大时,D、E、F都是中点,分两种情形讨论即 可解决问题;
(1)如图①中,
∵C(6,0),
∴BC=6
在等边三角形ABC中,AB=BC=AC=6,∠A=∠B=∠C=60°,
由题意知,当0<t<6时,AD=BE=CF=t,
∴BD=CE=AF=6﹣t,
∴△ADF≌△CFE≌△BED(SAS),
∴EF=DF=DE,
∴△DEF是等边三角形,
∴不论t如何变化,△DEF始终为等边三角形;

(2)如图②中,作AH⊥BC于H,则AH=ABsin60°=3![]() ,
,

∴S△AEC=![]() ×3
×3![]() ×(6﹣t)=
×(6﹣t)=![]() ,
,
∵EQ∥AB,
∴△CEQ∽△ABC,
∴![]() =(
=(![]() )2=
)2=![]() ,即S△CEQ=
,即S△CEQ=![]() S△ABC=
S△ABC=![]() ×9
×9![]() =
=![]() ,
,
∴S△AEQ=S△AEC﹣S△CEQ=![]() ﹣
﹣![]() =﹣
=﹣![]() (t﹣3)2+
(t﹣3)2+![]() ,
,
∵a=﹣![]() <0,
<0,
∴抛物线开口向下,有最大值,
∴当t=3时,△AEQ的面积最大为![]() cm2,
cm2,
(3)如图③中,由(2)知,E点为BC的中点,线段EQ为△ABC的中位线,

当AD为菱形的边时,可得P1(3,0),P3(6,3![]() ),
),
当AD为对角线时,P2(0,3![]() ),
),
综上所述,满足条件的点P坐标为(3,0)或(6,3![]() )或(0,3
)或(0,3![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O中,AB为弦,直线PO交⊙O于点M、N,PO⊥AB于C,过点B作直径BD,连接AD、BM、AP.
(1)求证:PM∥AD;
(2)若∠BAP=2∠M,求证:PA是⊙O的切线;
(3)若AD=6,tan∠M=
 ,求⊙O的直径.
,求⊙O的直径.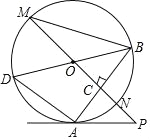
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b与x轴和y轴交于A、B两点,AB=4
 ,∠BAO=45°.
,∠BAO=45°.
(1)如图1,求直线AB的解析式.
(2)如图1,直线y=2x﹣2交x轴于点E.且P为该直线在直线AB上方一动点,当△PAB的面积等于10时,将线段PE沿着x轴平移得到线段P1E1,连接OP1.求OP1+P1E1+
 的最小值.
的最小值.(3)如图2,在(2)问的条件下,若直线y=2x﹣2与y轴的交点是C,连接CE1,得到△OCE1,将△OCE1绕着原点O逆时针旋转α°(0<α<180),旋转过程中直线OC与直线AB交于点M,直线CE1与直线AB交于点N,当△CMN为等腰三角形时,直接写出α的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点O为△ABC的两条角平分线的交点,过点O作OD⊥BC,垂足为D,且OD=4.若△ABC的面积是34,则△ABC的周长为( )

A.8.5B.15C.17D.34
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,在平面直角坐标系中,对
 进行循环往复的轴对称变换,若原来点A坐标是
进行循环往复的轴对称变换,若原来点A坐标是 ,则经过第2019次变换后所得的A点坐标是________.
,则经过第2019次变换后所得的A点坐标是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= .

-
科目: 来源: 题型:
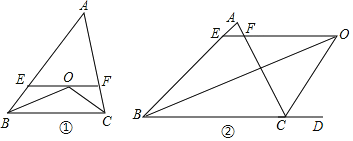
查看答案和解析>>【题目】(1)如图①,△ABC中,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于点E、F,试猜想EF、BE、CF之间有怎样的关系,并说明理由;
(2)如图,若将图①中∠ACB的平分线改为外角∠ACD的平分线,其它条件不变,请直接写出EF、BE、CF之间的关系 .
相关试题

