【题目】如图,在△ABC中,AC=BC,以BC边为直径作⊙O交AB边于点D,过点D作DE⊥AC于点E.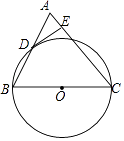
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径等于 ![]() ,cosB=
,cosB= ![]() ,求线段DE的长.
,求线段DE的长.
参考答案:
【答案】
(1)解:证明:连结OD.
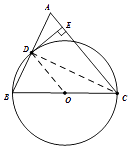
∵AC=BC,
∴∠A=∠B,
∵OB=OD,
∴∠B=∠ODB,
∴∠A=∠ODB,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线,
(2)解:如图,连结CD.

∵⊙O的半径等于 ![]() ,
,
∴BC=3,∠CDB=90°,
在Rt△CDB中,
cosB= ![]() =
= ![]() ,
,
∴BD=1, ![]() ,
,
∵AC=BC=3,∠CDB=90°.
∴AD=BD=1,
解法一:在Rt△ADC中, ![]() ,
,
解法二:∵∠A=∠A,∠ADC=∠AED=90°,
∴△ACD∽△ADE.
∴ ![]() .
.
∴ ![]()
【解析】(1)根据等腰三角形的性质,等边对等角,得到角相等,得出平行线,得出DE是⊙O的切线;(2)根据在Rt△CDB中,由三角函数和勾股定理求出AC=BC、CD、AD=BD的值,由角相等得出△ACD∽△ADE,得到比例,求出DE的值.
【考点精析】通过灵活运用等腰三角形的性质和解直角三角形,掌握等腰三角形的两个底角相等(简称:等边对等角);解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y1=kx+2与反比例函数y2=
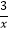 的图象交于点A(m,3),与坐标轴分别交于B,C两点.
的图象交于点A(m,3),与坐标轴分别交于B,C两点.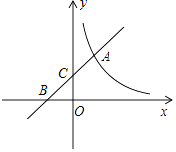
(1)若y1>y2>0,求自变量x的取值范围;
(2)动点P(n,0)在x轴上运动,当n为何值时,|PA﹣PC|的值最大?并求最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离
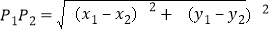 .例如P1(2,-4)、P2(7,8),其两点间的距离
.例如P1(2,-4)、P2(7,8),其两点间的距离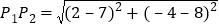 ,同时,当两点所在的直线再坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线再坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.(1)已知A(2,4)、B(-3,-8),试求A、B两点间的距离____.
(2)已知M、N在平行于y轴的直线上,点M的纵坐标为4,点N的纵坐标为-1,试求M、N 两点的距离为 .
(3)已知一个三角形各顶点坐标为D(1,6)、E(-2,2)、F(4,2),你能判定此三角形的形状吗?说明理由.
(4)在(3)的条件下,平面直角坐标中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标及PD+PF的最短长度.
-
科目: 来源: 题型:
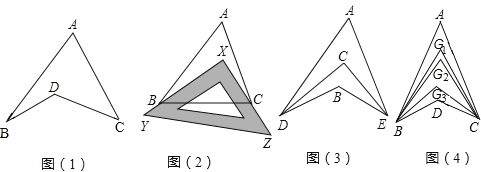
查看答案和解析>>【题目】探究与发现:如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”.
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX= °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】材料1:把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式因式分解.例如:
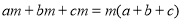 ,
,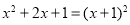 都是因式分解.因式分解也可称为分解因式.
都是因式分解.因式分解也可称为分解因式.材料2:只含有一个未知数,且未知数的最高次数是
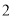 的整式方程称作一元二次方程.一元二次方程的般形式是:
的整式方程称作一元二次方程.一元二次方程的般形式是: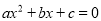 (其中
(其中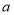 ,
,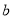 ,
,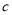 为常数且
为常数且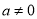 ).“转化”是一种重要的数学思想方法,我们可以利用因式分解把部分一元二次方程转化为一元一次方程求解.
).“转化”是一种重要的数学思想方法,我们可以利用因式分解把部分一元二次方程转化为一元一次方程求解.例如解方程;
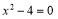
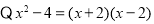
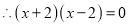
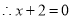 或
或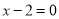
 原方程的解是
原方程的解是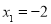 ,
,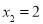
∴原方程的解是
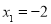 ,
,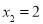
又如解方程:
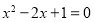
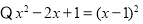
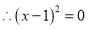

 原方程的解是
原方程的解是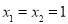
请阅读以上材料回答以下问题:
(1)若
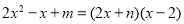 ,则
,则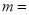 _______;
_______;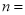 _______;
_______;(2)请将下列多项式因式分解:
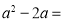 _______,
_______, ________;
________;(3)在平面直角坐标系中,已知点
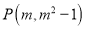 ,
,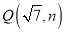 ,其中
,其中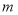 是一元二次方程
是一元二次方程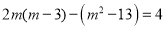 的解,
的解,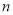 为任意实数,求
为任意实数,求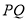 长度的最小值.
长度的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)已知:
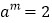 ,
,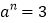 ,求
,求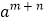 的值.
的值.(2)已知:
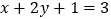 ,求
,求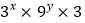 的值.
的值.(3)已知:
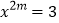 ,
,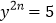 ,求
,求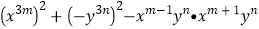 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.
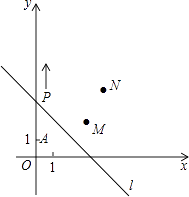
(1)当t=2时,则AP= , 此时点P的坐标是 .
(2)当t=3时,求过点P的直线l:y=﹣x+b的解析式?
(3)当直线l:y=﹣x+b从经过点M到点N时,求此时点P向上移动多少秒?
(4)点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 .
相关试题

