【题目】如图,直线y1=kx+2与反比例函数y2= ![]() 的图象交于点A(m,3),与坐标轴分别交于B,C两点.
的图象交于点A(m,3),与坐标轴分别交于B,C两点.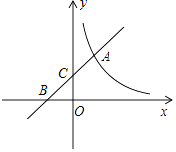
(1)若y1>y2>0,求自变量x的取值范围;
(2)动点P(n,0)在x轴上运动,当n为何值时,|PA﹣PC|的值最大?并求最大值.
参考答案:
【答案】
(1)解:当y2= ![]() =3时,x=1,
=3时,x=1,
∴点A的坐标为(1,3).
观察函数图象,可知:当x>1时,直线在双曲线上方,
∴若y1>y2>0,自变量x的取值范围为x>1.
(2)解:将A(1,3)代入y1=kx+2中,
3=k+2,解得:k=1,
∴直线AB的解析式为y1=x+2.
当x=0时,y1=x+2=2,
∴点C的坐标为(0,2),
∴AC= ![]() =
= ![]() .
.
当y1=x+2=0时,x=﹣2,
∴点B的坐标为(﹣2,0).
当点P于点B重合时,|PA﹣PC|的值最大,此时n=﹣2,|PA﹣PC|=AC= ![]() .
.
∴当n为﹣2时,|PA﹣PC|的值最大,最大值为 ![]() .
.
【解析】(1)把点A(m,3),代入反比例函数的解析式,求出m的值,观察函数图象,可知当x>1时,直线在双曲线上方,求出自变量x的取值范围即可;(2)将A(1,3)代入直线解析式,求出直线AB的解析式,得到点C的坐标,根据两点间的距离求出AC的值,得到点B的坐标,求出|PA﹣PC|的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD2=ABAE.
求证:DE是⊙O的切线.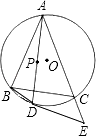
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:
七年级(3)班学生到图书馆的次数统计表到图书馆的
次数0次
1次
2次
3次
4次及
以上人数
5
10
m
8
12
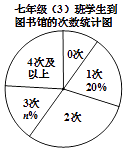
(1)求图表中m,n的值;
(2)该年级学生共有300人,估计这周到图书馆的次数为“4次及以上”的学生大约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,∠ACB=90°,CD⊥AB于D,BE:AB=3:5,若CE=
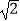 ,cos∠ACD=
,cos∠ACD= 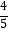 ,求tan∠AEC的值及CD的长.
,求tan∠AEC的值及CD的长.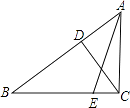
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离
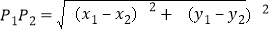 .例如P1(2,-4)、P2(7,8),其两点间的距离
.例如P1(2,-4)、P2(7,8),其两点间的距离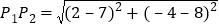 ,同时,当两点所在的直线再坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线再坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.(1)已知A(2,4)、B(-3,-8),试求A、B两点间的距离____.
(2)已知M、N在平行于y轴的直线上,点M的纵坐标为4,点N的纵坐标为-1,试求M、N 两点的距离为 .
(3)已知一个三角形各顶点坐标为D(1,6)、E(-2,2)、F(4,2),你能判定此三角形的形状吗?说明理由.
(4)在(3)的条件下,平面直角坐标中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标及PD+PF的最短长度.
-
科目: 来源: 题型:
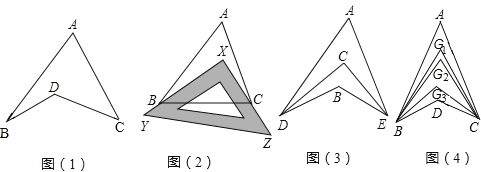
查看答案和解析>>【题目】探究与发现:如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”.
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX= °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,以BC边为直径作⊙O交AB边于点D,过点D作DE⊥AC于点E.
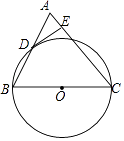
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径等于 ,cosB=
,cosB=  ,求线段DE的长.
,求线段DE的长.
相关试题

