【题目】如图所示,正比例函数 ![]() 的图象与反比例函数
的图象与反比例函数 ![]()
![]() 在第一象限的图象交于点
在第一象限的图象交于点 ![]() ,过点
,过点 ![]() 作
作 ![]() 轴的垂线,垂足为
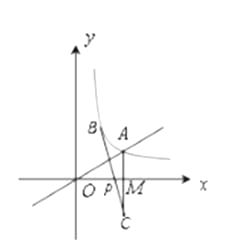
轴的垂线,垂足为 ![]() ,已知△OAM的面积为1.
,已知△OAM的面积为1.
(1)求反比例函数的解析式;
(2)如果点 ![]() 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点 ![]() 与点
与点 ![]() 不重合),且点
不重合),且点 ![]() 的横坐标为1,在
的横坐标为1,在 ![]() 轴上求一点
轴上求一点 ![]() ,使
,使 ![]() 最小.
最小.
参考答案:
【答案】
(1)解:设A点的坐标为( ![]() ,
, ![]() ),
),
则 ![]() .∴
.∴ ![]() .
.
∵ ![]() ,∴
,∴ ![]() .∴
.∴ ![]() .
.
∴反比例函数的解析式为 ![]()
(2)解: 由 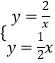 得
得 ![]() 或
或 ![]() ∴A为
∴A为 ![]() .
.
设A点关于 ![]() 轴的对称点为C,则C点的坐标为
轴的对称点为C,则C点的坐标为 ![]() .
.
如要在 ![]() 轴上求一点P,使PA+PB最小.则P点应为BC和x轴的交点,如图所示.
轴上求一点P,使PA+PB最小.则P点应为BC和x轴的交点,如图所示.
令直线BC的解析式为 ![]() .
.
∵B为(1,2),∴ ![]() ∴
∴ ![]()
∴BC的解析式为 ![]() .
.
当 ![]() 时,
时, ![]() .∴P点坐标为
.∴P点坐标为 ![]() .
.
【解析】(1)根据反比例函数k的几何意义,由已知△OAM的面积为1,设A点的坐标为( a , b ),得出![]() a b = 1,即可求出k(k>0)的值,从而得出反比例函数的解析式。
a b = 1,即可求出k(k>0)的值,从而得出反比例函数的解析式。
(2)此题是在 x 轴上求一点 P ,使 P A + P B 最小,根据轴对称的性质,先作出A点关于 x 轴的对称点为C,连接BC交x轴于点P,可得出点C的坐标,再求出直线BC的函数解析式,根据y=0,求出对应的自变量的值,即可得出点P的坐标。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对反比例函数的性质的理解,了解性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
-
科目: 来源: 题型:
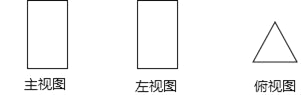
查看答案和解析>>【题目】已知如图为一几何体的三视图:主视图和左视图都是长方形,俯视图是等边三角形
(1)写出这个几何体的名称;
(2)若主视图的高为10cm,俯视图中三角形的边长为4cm,求这个几何体的侧面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上点A对应的数为a,点B对应的数为b,且多项式﹣
 x2y﹣
x2y﹣ xy2﹣2xy+5的次数为a,常数项为b.
xy2﹣2xy+5的次数为a,常数项为b.(1)直接写出a、b的值;
(2)数轴上点A、B之间有一动点P(不与A、B重合),若点P对应的数为x,试化简:|2x+6|+4|x﹣5|﹣|6﹣x|+|3x﹣9|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:
单价x(元/件)
30
34
38
40
42
销量y(件)
40
32
24
20
16
(1)通过对上面表格中的数据进行分析,发现销量 (件)与单价
(件)与单价  (元/件)之间存在一次函数关系,求
(元/件)之间存在一次函数关系,求  关于
关于  的函数关系式(不需要写出函数自变量的取值范围);
的函数关系式(不需要写出函数自变量的取值范围);
(2)预计在今后的销售中,销量与单价仍然存在(1)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】解答下面的问题:
(1)如果a2+a=3,求a2+a+2015的值.
(2)已知a﹣b=﹣3,求3(b﹣a)2﹣5a+5b+5的值.
(3)已知a2+2ab=﹣3,ab﹣b2=﹣5,求4a2+
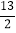 ab+
ab+ b2的值.
b2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】x1、x2、x3、…x20是20个由1,0,﹣1组成的数,且满足:①x1+x2+x3+…+x20=4,②(x1﹣1)2+(x2﹣1)2+(x3﹣1)2…+(x20﹣1)2=32,则这列数中1的个数为_____个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.

(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
相关试题

