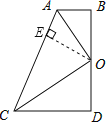
【题目】如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.
(1)求证:OC平分∠ACD;
(2)求证:OA⊥OC.

参考答案:
【答案】(1)见解析;(2)见解析
【解析】
(1)过点O作OE⊥AC于E,根据角平分线的性质可得OB=OE,求出OE=OD,然后根据到角的两边距离相等的点在角的平分线上证明即可;
(2)利用“HL”证明△ABO和△AEO全等,可得∠AOB=∠AOE,同理∠COD=∠COE,然后求出∠AOC=90°,再根据垂直的定义即可证明.
证明:(1)过点O作OE⊥AC于E,
∵∠ABD=90°,OA平分∠BAC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD,
∵∠D=90°,
∴OD⊥CD,
∴OC平分∠ACD;
(2)在Rt△ABO和Rt△AEO中,
![]() ,
,
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE,
同理得:∠COD=∠COE,
∴∠AOC=∠AOE+∠COE=![]() ×180°=90°,
×180°=90°,
∴OA⊥OC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个互相重合的直角三角形,将其中的一个三角形沿点
 到
到 的方向平移到
的方向平移到 的位置,若
的位置,若 ,
, ,且平移的距离为6,则阴影部分面积是_______.
,且平移的距离为6,则阴影部分面积是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,线段
 直线
直线 ,垂足为
,垂足为 ,平移线段
,平移线段 ,使点
,使点 与点
与点 重合,点
重合,点 的对应点记为点
的对应点记为点 .
.
操作与思考:
(1)画出线段
 和直线
和直线 ;
;(2)直线
 与
与 的位置关系是_______,理由是:____________________________;
的位置关系是_______,理由是:____________________________;线段
 与
与 的数量关系是_______,理由是:____________________________.
的数量关系是_______,理由是:____________________________.实践与应用:
(3)如图,等边
 和等边
和等边 的面积分别为3和5,点
的面积分别为3和5,点 、
、 、
、 在一直线上,则
在一直线上,则 的面积是_____________.
的面积是_____________.
(4)如图,网格中每个小正方形的边长为1,请用三种不同方法,求出
 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,则y1 , y2 , 0的大小关系是( )
A.0<y1<y2
B.y1<0<y2
C.y1<y2<0
D.y2<0<y1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( )
A.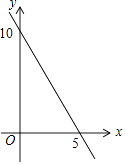
B.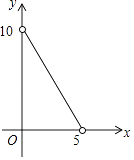
C.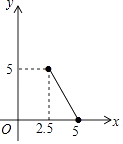
D.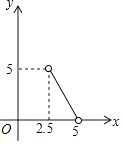
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
(1)求证:AD⊥CF;
(2)连接AF,试判断△ACF的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将2×2的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上,若直线y=kx(k≠0)与正方形ABCD有公共点,则k不可能是( )

A.3
B.2
C.1
D.
相关试题

