【题目】在数轴上两点之向的距离两数差的绝对值,我们可以用表示这两个点的大写字母一起标记,比如,表示点A的数为2,点B表示的数为﹣3,点A与点B之间的距离记作AB,别AB=2﹣(﹣3)=5.
(1)数轴上表示﹣3和5的两点之间的距离是
(2)如图,在数轴上点A表示数a,点C表示数c,且|a+20|+(c﹣30)2=0.求点A与点C之间的距离AC;
(3)在(2)的条件下,在数轴上是否存在点B,使AB=5,若存在,求出点B表示的数b;若不存在,请说明理由.
![]()
参考答案:
【答案】(1) 8;(2)50;(3) ﹣15或﹣25
【解析】
(1)根据数轴上两点间的距离公式,即可求出结论;
(2)利用绝对值及偶次方的非负性,即可求出a,b的值,再利用数轴上两点间的距离公式,即可求出AC的值;
(3)根据数轴上两点间的距离公式结合AB=5,即可得出关于b的含绝对值符号的一元一次方程,解之即可得出结论.
(1)5﹣(﹣3)=8.
(2)∵|a+20|+(c﹣30)2=0,
∴a=﹣20,c=30,
∴AC=30﹣(﹣20)=50.
(3)根据题意得:|b﹣(﹣20)|=5,
解得:b1=﹣15,b2=﹣25.
答:点B表示的数b为﹣15或﹣25.
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=45°,BD=2时,求D,F两点间的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家、食堂、图书馆依次在同一条直线上,小明从家去食堂吃早餐,接着云图书馆读报,然后回家。如图反映了这个过程,小明离家的距离与时间之间的对应关系,下列说法错误的是( )
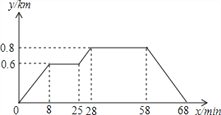
A. 小明从家到食堂用了8min B. 小明家离食堂0.6km,食堂离图书馆0.2km
C. 小明吃早餐用了30min,读报用了17min D. 小明从图书馆回家的平均速度为0.08km/min
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P的坐标为(a,b),点P的“变换点”P`的坐标定义如下:当
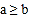 时,P`点坐标为(a,-b);当
时,P`点坐标为(a,-b);当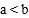 时,P`点坐标为(b,-a)。线段l:
时,P`点坐标为(b,-a)。线段l: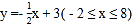 上所有点按上述“变换点”组成一个新的图形,若直线
上所有点按上述“变换点”组成一个新的图形,若直线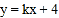 与组成的新的图形有两个交点,则k的取值范围是( )
与组成的新的图形有两个交点,则k的取值范围是( )A.
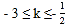 B.
B. 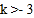 或
或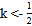 C.
C. 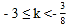 D.
D. 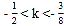
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个装有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单价:min)之间的关系如图所示。在第_______分钟时该容器内的水恰好为10L.

-
科目: 来源: 题型:
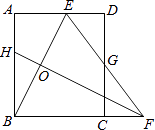
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是 .
相关试题

