【题目】在平面直角坐标系中,点P的坐标为(a,b),点P的“变换点”P`的坐标定义如下:当![]() 时,P`点坐标为(a,-b);当
时,P`点坐标为(a,-b);当![]() 时,P`点坐标为(b,-a)。线段l:
时,P`点坐标为(b,-a)。线段l:![]() 上所有点按上述“变换点”组成一个新的图形,若直线
上所有点按上述“变换点”组成一个新的图形,若直线![]() 与组成的新的图形有两个交点,则k的取值范围是( )
与组成的新的图形有两个交点,则k的取值范围是( )
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】
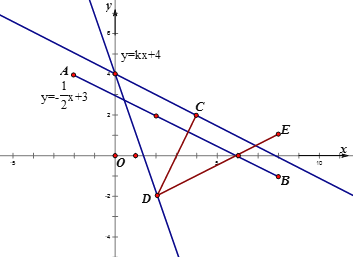
根据题意画出图形,确定变换分界点,根据条件,从直线y=kx+4的变动范围确定k的取值范围.
由a≥b,得x≥![]() ,解得x≥2,
,解得x≥2,
所以,线段变换的分界点是(2,2)
当a≥b,变换得到新图形是线段DE;当a<b时,变换得到新图形是线段DC.
且D(2,-2),C(4,2),E(8,2).
直线y=kx+4与y轴相交于(0,4),如图,假如直线与新图形有两个交点,那么2<x<4,-2<y<2.
因为![]() ,
,
所以,由上述可得![]() ,
,
即![]() ,
,
![]()
故选:A
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=45°,BD=2时,求D,F两点间的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家、食堂、图书馆依次在同一条直线上,小明从家去食堂吃早餐,接着云图书馆读报,然后回家。如图反映了这个过程,小明离家的距离与时间之间的对应关系,下列说法错误的是( )
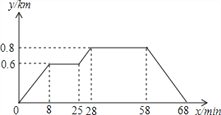
A. 小明从家到食堂用了8min B. 小明家离食堂0.6km,食堂离图书馆0.2km
C. 小明吃早餐用了30min,读报用了17min D. 小明从图书馆回家的平均速度为0.08km/min
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上两点之向的距离两数差的绝对值,我们可以用表示这两个点的大写字母一起标记,比如,表示点A的数为2,点B表示的数为﹣3,点A与点B之间的距离记作AB,别AB=2﹣(﹣3)=5.
(1)数轴上表示﹣3和5的两点之间的距离是
(2)如图,在数轴上点A表示数a,点C表示数c,且|a+20|+(c﹣30)2=0.求点A与点C之间的距离AC;
(3)在(2)的条件下,在数轴上是否存在点B,使AB=5,若存在,求出点B表示的数b;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个装有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单价:min)之间的关系如图所示。在第_______分钟时该容器内的水恰好为10L.

-
科目: 来源: 题型:
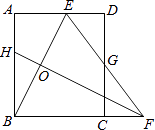
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图2是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°,折线NG﹣GH﹣HE﹣EF表示楼梯,GH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边都相切,且AO∥GH.

(1)如图2①,若点H在线段OB时,则 的值是;
的值是;
(2)如果一级楼梯的高度HE=(8 +2)cm,点H到线段OB的距离d满足条件d≤3cm,那么小轮子半径r的取值范围是 .
+2)cm,点H到线段OB的距离d满足条件d≤3cm,那么小轮子半径r的取值范围是 .
相关试题

