【题目】在△ABC中,∠ACB=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D,E,F是垂足,且AB=5,BC=4,AC=3,则点O到三边AB,AC,BC的距离分别是( )
A. 1,1,1 B. 2,2,2 C. 1,1.5,2 D. 无法确定
参考答案:
【答案】A
【解析】
由角平分线的性质易得OE=OF=OD,AE=AF,CE=CD,BD=BF,设OE=OF=OD=x,则CE=CD=x,BD=BF=4-x,AF=AE=3-x,所以3-x+4-x=5,解答即可.
连接OB,如图所示:
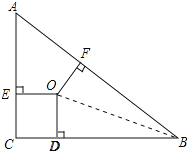
∵点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,
∴OE=OF=OD,
在△BOF与△BOD中,
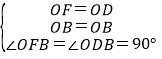 ,
,
∴Rt△BOF≌Rt△BOD(HL),
∴BD=BF,
同理可证:AE=AF,CE=CD,
∵∠C=90°,OD⊥BC,OE⊥AC,OF⊥AB,OD=OE,
∴OECD是正方形,
设OE=OF=OD=x,则CE=CD=x,BD=BF=4-x,AF=AE=3-x,
∴BF+FA=AB=5,即3-x+4-x=5,
解得x=1,
则OE=OF=OD=1,
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
C类表示“听同学讲过”,D类表示“不知道”,划分类别后的数据整理如表:类别
A
B
C
D
频数
30
40
24
b
频率
a
0.4
0.24
0.06
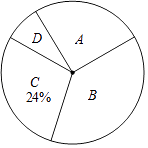
(1)表中的a=b=;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=∠AGE,∠D=∠DGC.
(1)试说明AB∥CD;
(2)若∠1+∠2=180°,且∠BEC=2∠B+60°,求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形OABC的边OC、OA分别在x轴、y轴上,B点在第一象限,点A的坐标是(0,4),OC=8.
(1)直接写出点B、C的坐标;
(2)点P从原点O出发,在边OC上以每秒1个单位长度的速度匀速向C点移动,同时点Q从点B出发,在边BA上以每秒2个单位长度的速度匀速向A点移动,当一个点到达终点时,另一个点随之停止移动,设移动的时间为t秒钟,探究下列问题:
① 当t值为多少时,直线PQ∥y轴?
② 在整个运动过程中,能否使得四边形BCPQ的面积是长方形OABC的面积的
 ?若能,请直接写出P、Q两点的坐标;若不能,说明理由.
?若能,请直接写出P、Q两点的坐标;若不能,说明理由.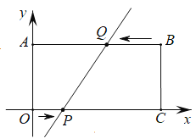
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=70°,∠ABC,∠ACB的平分线相交于点I,则∠BIC=_______________.
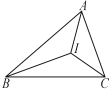
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB<BC.
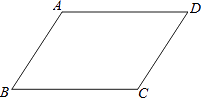
(1)利用尺规作图,在AD边上确定点E,使点E到边AB,BC的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,则DE= . -
科目: 来源: 题型:
查看答案和解析>>【题目】现有边长相等的正三角形、正方形、正六进形、正八边形形状的地砖,如果选择其中的两钟铺满平整的地面,那么选择的两种地砖形状不能是( )
A. 正三角形与正方形 B. 正三角形与正六边形
C. 正方形与正六边形 D. 正方形与正八边形
相关试题

