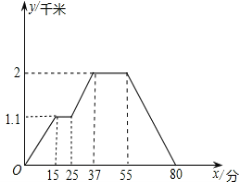
【题目】下图反映的过程是王老师步行从家去书店买书,又去超市买菜, 然后回家.其中x表示时间,y表示王老师离家的距离.根据图象回答下列问题:
(1)书店离王老师家多远?王老师从家到书店用了多少时间?
(2)超市离书店多远?超市离王老师家多远?王老师从超市走回家平均速度是多少?
参考答案:
【答案】(1)1.1千米,15分钟;(2)0.9千米,2千米,80米/分.
【解析】
(1)小明第一个到达的地方应是书店,也应是第一次路程不再增加的开始,所对应的时间为15分,路程为1.1千米.
(2)小明第二个到达的地方应是超市,也应是第二次路程不再增加的开始,所对应的路程为2千米,那么距离超市应是2-1.1(千米):买菜所用时间应是第二次与x轴平行的线段所对应的时间的差:55-37(分钟);超市就是小明到达的最远的地方,平均速度=总路程÷总时间.
解:(1)由图象可以看出书店离小明家1.1千米,小明走到书店用了15分;
(2)超市离书店:2-1.1=0.9(千米),小明在超市用了55-37=18(分);由图象可以看出超市离小明家2千米,小明从书店走回家的平均速度是![]() =80米/分.
=80米/分.
答:(1)书店离王老师家1.1千米,王老师从家到书店用了15分;
(2)超市离书店0.9千米,超市离王老师家2千米,王老师从超市走回家平均速度是80米/分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形APQ.
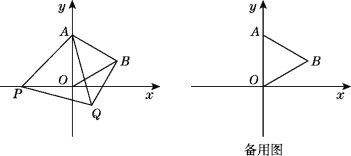
(1)求点B的坐标.
(2)在点P运动过程中,∠ABQ的大小是否发生改变?若不改变,求出其大小;若改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
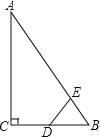
A.2B.2.5或3.5
C.3.5或4.5D.2或3.5或4.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
(1)正比例函数
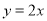 过( 0 , )和( 1 , );
过( 0 , )和( 1 , );(2)一次函数
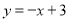 ( 0 , )( , 0 ).
( 0 , )( , 0 ).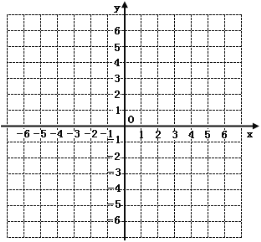
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
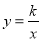 (k<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到了点B’在此反比例函数的图象上,则t的值是( )
(k<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到了点B’在此反比例函数的图象上,则t的值是( )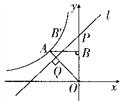
A.
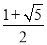 B.
B. 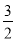 C.
C. 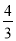 D.
D. 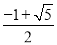
-
科目: 来源: 题型:
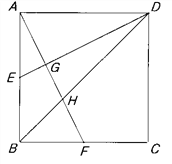
查看答案和解析>>【题目】正方形ABCD中,E,F分别是AB与BC边上的中点,连接AF,DE,BD,交于G,H(如图所示)。求AG:GH:HF的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
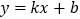 的图象与反比例函数
的图象与反比例函数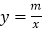 的图象交于
的图象交于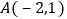 ,
,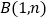 两点.
两点.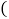 Ⅰ
Ⅰ 试确定上述反比例函数和一次函数的表达式;
试确定上述反比例函数和一次函数的表达式; Ⅱ
Ⅱ 连OB,在x轴上取点C,使
连OB,在x轴上取点C,使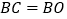 ,并求
,并求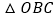 的面积;
的面积;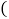 Ⅲ
Ⅲ 直接写出一次函数值大于反比例函数值的自变量x的取值范围.
直接写出一次函数值大于反比例函数值的自变量x的取值范围.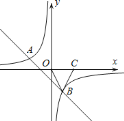
相关试题

