【题目】AD为△ABC边上 BC上的中线,若 AD=4,AC=5,则 AB的取值范围是___________
参考答案:
【答案】3<AB<13
【解析】
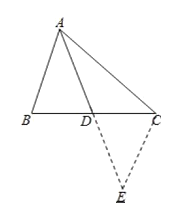
延长AD到E,使DE=AD,连接CE,利用“边角边”证明△ABD和△ECD全等,再根据全等三角形对应边相等可得CE=AB,然后根据三角形的任意两边之和大于第三边,两边之差小于第三边解答.
延长AD到E,使DE=AD,连接CE,
则AE=2AD=2×4=8,
∵AD是BC边上的中线,
∴BD=CD,
∵在△ABD和△ECD中,
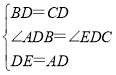 ,
,
∴△ABD≌△ECD(SAS),
∴CE=AB,
又∵AC=5,
∴5+8=13,85=3,
∴3<CE<13,
即AB的取值范围是:3<AB<13.
故答案为:3<AB<13.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,A(-3,0)、B(0,4)、P(4,0),AB=5,M、N两点分别在线段 AB、y轴上,则 PN+MN的最小值为( )
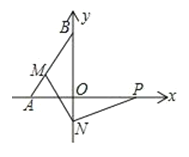
A.4B.
 C.
C.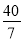 D.5
D.5 -
科目: 来源: 题型:
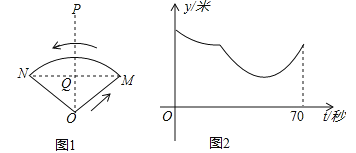
查看答案和解析>>【题目】小阳在如图①所示的扇形舞台上沿O-M-N匀速行走,他从点O出发,沿箭头所示的方向经过点M再走到点N,共用时70秒.有一台摄像机选择了一个固定的位置记录了小阳的走路过程,设小阳走路的时间为t(单位:秒),他与摄像机的距离为y(单位:米),表示y与t的函数关系的图象大致如图②,则这个固定位置可能是图①中的点_______(在点P、N、Q、M、O中选取)
-
科目: 来源: 题型:
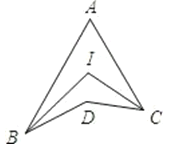
查看答案和解析>>【题目】如图 ,BI、CI分别平分∠ABD和∠ACD,∠A=40°,∠D=160°,则∠I=___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
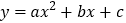 的图象与x轴交于(
的图象与x轴交于(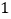 , 0)和(
, 0)和(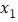 , 0), 其中
, 0), 其中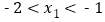 ,与
,与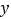 轴交于正半轴上一点.下列结论:①
轴交于正半轴上一点.下列结论:① ;②
;②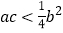 ;③a>b;④
;③a>b;④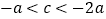 .其中正确结论的序号是____________.
.其中正确结论的序号是____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】有三条长度均为a的线段,分别按以下要求画圆.
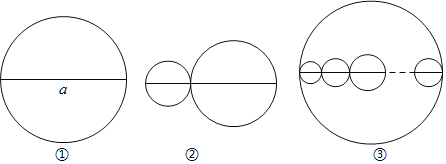
(1)如图①,以该线段为直径画一个圆,记该圆的周长为C1;如图②,在该线段上任取一点,再分别以两条小线段为直径画两个圆,这两个圆的周长的和为C2,请指出C1和C2的数量关系,并说明理由;
(2)如图③,当a=11时,以该线段为直径画一个大圆,再在大圆内画若千小圆,这些小圆的直径都和大圆的直径在同一条直线上,且小圆的直径的和等于大圆的直径,那么图中所有小圆的周长的和为 .(直接填写答案,结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,O,B三点在同一直线上,∠BOD与∠BOC互补.
(1)∠AOC与∠BOD的度数相等吗,为什么?
(2)已知OM平分∠AOC,若射线ON在∠COD的内部,且满足∠AOC与∠MON互余;
①∠AOC=32°,求∠MON的度数;
②试探究∠AON与∠DON之间有怎样的数量关系,请写出结论并说明理由.

相关试题

