【题目】(本小题满分10分)已知关于x的方程mx2-(3m-1)x+2m-2=0
(1)求证:无论m取任何实数时,方程恒有实数根.
(2)若关于x的二次函数y= mx2-(3m-1)x+2m-2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
(3)在直角坐标系xoy中,画出(2)中的函数图象,结合图象回答问题:当直线y=x+b与(2)中的函数图象只有两个交点时,求b的取值范围.
参考答案:
【答案】
(1)略
(2)y1= x(x-2)或y2=![]() (x-2)(x-4)
(x-2)(x-4)
(3)当b<-或b>-或b=-2时,直线y=x+b与(2)中的图象只有两个交点
【解析】解:(1)分两种情况讨论:
①当m=0时,方程为x-2=0,∴x=2 方程有实数根
②当m≠0时,则一元二次方程的根的判别式
△=[-(3m-1)]2-4m(2m-2)=m2+2m+1=(m+1)2≥0
不论m为何实数,△≥0成立,∴方程恒有实数根
综合①②,可知m取任何实数,方程mx2-(3m-1)x+2m-2=0恒有实数根.
(2)设x1,x2为抛物线y= mx2-(3m-1)x+2m-2与x轴交点的横坐标.
则有x1+x2=![]() ,x1·x2=
,x1·x2=![]()
由| x1-x2|=![]() =
=![]() =
=![]() =
=![]() ,
,
由| x1-x2|=2得![]() =2,∴
=2,∴![]() =2或
=2或![]() =-2
=-2
∴m=1或m=![]()
∴所求抛物线的解析式为:y1=x2-2x或y2=![]() x2+2x-
x2+2x-
即y1= x(x-2)或y2=![]() (x-2)(x-4)其图象如图所示.
(x-2)(x-4)其图象如图所示.
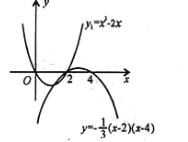
(3)在(2)的条件下,直线y=x+b与抛物线y1,y2组成的图象只有两个交点,结合图象,求b的取值范围.
 ,当y1=y时,得x2-3x-b=0,△=9+4b=0,解得b=-;
,当y1=y时,得x2-3x-b=0,△=9+4b=0,解得b=-;
同理 ,可得△=9-4(8+3b)=0,得b=-.
,可得△=9-4(8+3b)=0,得b=-.
观察函数图象可知当b<-或b>-时,直线y=x+b与(2)中的图象只有两个交点.
由![]()
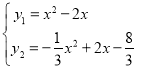
当y1=y2时,有x=2或x=1
当x=1时,y=-1
所以过两抛物线交点(1,-1),(2,0)的直线y=x-2,
综上:当b<-或b>-或b=-2时,直线y=x+b与(2)中的图象只有两个交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下面图形,解答问题:

(1)在△ABC中,AB=AC,∠BAC=100°,DE、FG分别是边AB、AC的垂直平分线(如图1),求∠DAG的度数?
(2)在(1)中,若去掉“AB=AC”的条件,其余条件不变(如图2),还能求出∠DAG的度数吗?若能,请求出∠DAG的度数;若不能,请说明理由;
(3)在(图2)的情况下试探索△ADG的周长与BC长的关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了利用图象法来求一元二次方程的近似根的知识后进行了尝试:在直角坐标系中作出二次函数
 的图象,由图象可知,方程
的图象,由图象可知,方程 有两个根,一个在
有两个根,一个在 和
和 之间,另一个在
之间,另一个在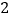 和
和 之间.利用计算器进行探索:由下表知,方程的一个近似根是( )
之间.利用计算器进行探索:由下表知,方程的一个近似根是( )









A. -4.1 B. -4.2 C. -4.3 D. -4.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】(11·湖州)如图,已知抛物线
 经过点(0,-3),请你确定一个
经过点(0,-3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间。你确定的b的值是 ▲
 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, △ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC
⑴求∠ECD的度数;
⑵若CE=5,求CB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
 ,其中
,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程
 的一根为
的一根为 .
. 求
求 关于
关于 的函数关系式;
的函数关系式; 求证:抛物线
求证:抛物线 与
与 轴有两个交点;
轴有两个交点; 设抛物线
设抛物线 与
与 轴交于
轴交于 、
、 两点(
两点( 、
、 不重合),且以
不重合),且以 为直径的圆正好经过该抛物线的顶点,求
为直径的圆正好经过该抛物线的顶点,求 ,
, 的值.
的值.
相关试题

