【题目】根据下面图形,解答问题:

(1)在△ABC中,AB=AC,∠BAC=100°,DE、FG分别是边AB、AC的垂直平分线(如图1),求∠DAG的度数?
(2)在(1)中,若去掉“AB=AC”的条件,其余条件不变(如图2),还能求出∠DAG的度数吗?若能,请求出∠DAG的度数;若不能,请说明理由;
(3)在(图2)的情况下试探索△ADG的周长与BC长的关系?
参考答案:
【答案】(1)20°;(2)能,∠DAG=20°,理由见解析;(3)AD+DG+AG=BC.
【解析】
(1)利用线段垂直平分线的性质求出∠BAM+∠NAC=80°,∠BAC=100°,易求解;
(2)利用线段垂直平分线的性质求出∠BAM+∠NAC=80°,∠BAC=100°,求出即可;
(3)根据等腰三角形的性质即可得到结论.
(1)∵DE垂直平分AB,
∴DA=DB,
∴∠B=∠BAD,
同理:GA=GC,∠C=∠GAC,
∵∠B+∠C+∠BAC=180°,∠BAC=100°,
∴∠B+∠C=80°,
∴∠BAD+∠GAC=80°,
∴∠DAG=∠BAC-(∠BAD+∠GAC)=100°-80°=20°;
(2)能,∠DAG=20°;
理由是:∵DE垂直平分AB,
∴DA=DB,
∴∠B=∠BAD,
同理:GA=GC,∠C=∠GAC,
∵∠B+∠C+∠BAC=180°,∠BAC=100°,
∴∠B+∠C=80°,
∴∠BAD+∠GAC=80°,
∴∠DAG=∠BAC-(∠BAD+∠GAC)=100°-80°=20°;
(3)由(2)知,AD=BD,AG=GC,
∴AD+DG+AG=BD+DG+GC=BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将两块大小相同的含30°角的直角三角板(∠BAC=∠B1A1C=30°)按图①的方式放置,固定三角板A1B1C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A1C交于点E,AC与A1B1交于点F,AB与A1B1交于点O.

(1)求证:△BCE≌△B1CF.
(2)当旋转角等于30°时,AB与A1B1垂直吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知
 是等腰直角三角形,
是等腰直角三角形, ,点D是BC的中点
,点D是BC的中点 作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG. 试猜想线段BG和AE的数量关系是______;
试猜想线段BG和AE的数量关系是______; 将正方形DEFG绕点D逆时针方向旋转
将正方形DEFG绕点D逆时针方向旋转 ,
, 判断
判断 中的结论是否仍然成立?请利用图2证明你的结论;
中的结论是否仍然成立?请利用图2证明你的结论; 若
若 ,当AE取最大值时,求AF的值.
,当AE取最大值时,求AF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC。

(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BCD的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了利用图象法来求一元二次方程的近似根的知识后进行了尝试:在直角坐标系中作出二次函数
 的图象,由图象可知,方程
的图象,由图象可知,方程 有两个根,一个在
有两个根,一个在 和
和 之间,另一个在
之间,另一个在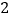 和
和 之间.利用计算器进行探索:由下表知,方程的一个近似根是( )
之间.利用计算器进行探索:由下表知,方程的一个近似根是( )









A. -4.1 B. -4.2 C. -4.3 D. -4.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】(11·湖州)如图,已知抛物线
 经过点(0,-3),请你确定一个
经过点(0,-3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间。你确定的b的值是 ▲
 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)已知关于x的方程mx2-(3m-1)x+2m-2=0
(1)求证:无论m取任何实数时,方程恒有实数根.
(2)若关于x的二次函数y= mx2-(3m-1)x+2m-2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
(3)在直角坐标系xoy中,画出(2)中的函数图象,结合图象回答问题:当直线y=x+b与(2)中的函数图象只有两个交点时,求b的取值范围.
相关试题

