【题目】在平面直角坐标系中,已知点A(-4,3),点B(-4,0),OA=5,以点O为直角顶点,点C在第一象限内,作等腰直角△AOC.
(1)直接写出点C坐标:
(2)直接写出四边形ABOC的面积:
(3)在y轴找一点P,使得△BOP的面积等于四边形ABOC的面积,请直接写出点P坐标:

参考答案:
【答案】(1)(3,4);(2)![]() ;(3)(0,
;(3)(0,![]() ),(
),(![]() ,
,![]() )
)
【解析】
(1)根据点绕原点顺时针旋转90°后坐标变化规律直接写出即可:点(m,n)绕原点顺时针旋转90°后坐标为(n,﹣m)
(2)四边形ABOC面积=△AOC面积+△ABO面积
(3)根据(2)的四边形面积去寻找△BOP以OB为底的合适的高即可
(1)∵点(m,n)绕原点顺时针旋转90°后坐标为(n,﹣m)
∴C坐标为(3,4)
(2)四边形ABOC面积=![]() =
=![]()
(3)由题设P距原点的距离为x
则:![]()
解得![]()
所以P的坐标为(0,![]() ),(
),(![]() ,
,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与坐标轴交于点
与坐标轴交于点 、
、 两点,直线
两点,直线 与直线
与直线 相交于点
相交于点 ,交
,交 轴于点
轴于点 ,且
,且 的面积为
的面积为 .
.
(1)求
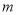 的值和点
的值和点 的坐标;
的坐标;(2)求直线
 的解析式;
的解析式;(3)若点
 是线段
是线段 上一动点,过点
上一动点,过点 作
作 轴交直线
轴交直线 于点
于点 ,
, 轴,
轴, 轴,垂足分别为点
轴,垂足分别为点 、
、 ,是否存在点
,是否存在点 ,使得四边形
,使得四边形 为正方形,若存在,请求出点
为正方形,若存在,请求出点 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】长春市市政工程中需要铺设一条长660米的管道,为了尽量减少施工对城市交通造成的影响,实际施工时,每天铺设管道的长度比原计划增加10%,结果提前6天完成,求实际每天铺设管道的长度与实际施工天数.某同学根据题意列出方程
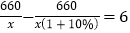 ,则方程中未知数x所表示的量是( )
,则方程中未知数x所表示的量是( )A. 原计划每天铺设管道的长度 B. 实际每天铺设管道的长度
C. 原计划施工的天数 D. 实际施工的天数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OABC的顶点A在y轴正半轴上,顶点C在x轴正半轴上,抛物线
 (a<0)的顶点为D,且经过点A、B.若△ABD为等腰直角三角形,则a的值为___________.
(a<0)的顶点为D,且经过点A、B.若△ABD为等腰直角三角形,则a的值为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.下列结论正确的个数是( )
(1)t=5时,s=150;(2)t=35时,s=450;(3)甲的速度是30米/分;(4)t=12.5时,s=0.

A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
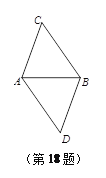
查看答案和解析>>【题目】如图,将线段AB绕点A逆时针旋转α度角得到线段AC,将线段AB绕点B逆时针旋转α度角得到线段BD(0°<α<180°),连结BC、AD.当α=_______度时,四边形ACBD是菱形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家自2016年1月1日起实行全面放开二胎政策,某计生组织为了解该市家庭对待这项政策的态度,准备采用以下调查方式中的一种进行调查:
A.从一个社区随机选取1 000户家庭调查;
B.从一个城镇的不同住宅楼中随机选取1 000户家庭调查;
C.从该市公安局户籍管理处随机抽取1 000户城乡家庭调查.
(1)在上述调查方式中,你认为比较合理的一个是【1】.(填“A”、“B”或“C”)
(2)将一种比较合理的调查方式调查得到的结果分为四类:(A)已有两个孩子;
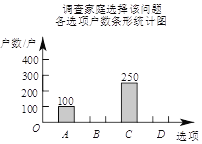
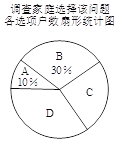
(B)决定生二胎;(C)考虑之中;(D)决定不生二胎.将调查结果绘制成如下两幅不完整的统计图.
请根据以上不完整的统计图提供的信息,解答下列问题:
①补全条形统计图.
②估计该市100万户家庭中决定不生二胎的家庭数.
相关试题

