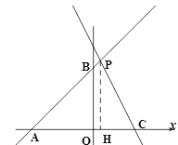
【题目】如图,直线![]() 与坐标轴交于点
与坐标轴交于点![]() 、
、![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积为
的面积为![]() .
.

(1)求![]() 的值和点
的值和点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析式;
的解析式;
(3)若点![]() 是线段
是线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,
,![]() 轴,
轴,![]() 轴,垂足分别为点
轴,垂足分别为点![]() 、
、![]() ,是否存在点
,是否存在点![]() ,使得四边形
,使得四边形![]() 为正方形,若存在,请求出点
为正方形,若存在,请求出点![]() 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ,
,![]() 点为
点为![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 点为
点为![]() ,理由见解析
,理由见解析
【解析】
(1)利用一次函数图象上点的坐标特征可求出m的值及点A的坐标;
(2)过点P作PH⊥x轴,垂足为H,则PH=![]() ,利用三角形的面积公式结合△PAC的面积为
,利用三角形的面积公式结合△PAC的面积为![]() ,可求出AC的长,进而可得出点C的坐标,再根据点P,C的坐标,利用待定系数法即可求出直线PC的解析式;
,可求出AC的长,进而可得出点C的坐标,再根据点P,C的坐标,利用待定系数法即可求出直线PC的解析式;
(3)由题意,可知:四边形EMNQ为矩形,设点E的纵坐标为t,利用一次函数图象上点的坐标特征可得出点E的坐标为(t-3,t)、点Q的坐标为(![]() ,t),利用正方形的性质可得出关于t的一元一次方程,解之即可得出结论.
,t),利用正方形的性质可得出关于t的一元一次方程,解之即可得出结论.
解:(1)把点![]() 代入直线
代入直线![]() ,
,
即 ![]() 时,
时,![]()
直线![]() ,当
,当![]() 时,
时,![]() 得:
得:![]()
![]() ,
,![]() 点为
点为![]()
(2)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,由(1)得,
,由(1)得,![]()
∴ ![]()
![]()
解得:![]()
![]()
![]() 点
点![]() 为
为![]()
设直线![]() 为
为![]() ,把点
,把点![]() 、
、![]() 代入,得:
代入,得:
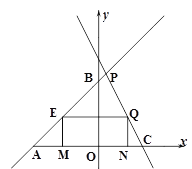
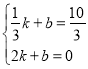 解得:
解得:![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
(3)由已知可得,四边形![]() 为矩形,
为矩形,
设点![]() 的纵坐标为
的纵坐标为![]() ,则
,则![]() 得:
得: ![]()
![]() 点为
点为![]()
![]() 轴
轴
![]() 点的纵坐标也为
点的纵坐标也为![]()
![]() 点在直线
点在直线![]() 上,当
上,当![]() 时,
时,![]()
![]()
![]()
又![]()
当![]() 时,矩形
时,矩形![]() 为正方形,所以
为正方形,所以![]()
![]()
故![]() 点为
点为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是( )
A. ①② B. ②③ C. ①③ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题背景】
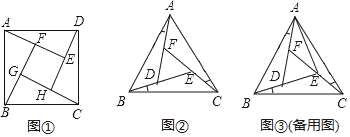
如图①所示,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
【类比研究】
如图②所示,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合).
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)连结AE,若AF=DF,AB=7,求△DEF的边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上移动,∠OAB的平分线与∠OBA的外角平分线交于点C,试猜想:随着点A,B的移动,∠ACB的大小是否发生变化,并说明理由.
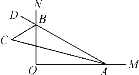
-
科目: 来源: 题型:
查看答案和解析>>【题目】长春市市政工程中需要铺设一条长660米的管道,为了尽量减少施工对城市交通造成的影响,实际施工时,每天铺设管道的长度比原计划增加10%,结果提前6天完成,求实际每天铺设管道的长度与实际施工天数.某同学根据题意列出方程
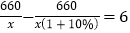 ,则方程中未知数x所表示的量是( )
,则方程中未知数x所表示的量是( )A. 原计划每天铺设管道的长度 B. 实际每天铺设管道的长度
C. 原计划施工的天数 D. 实际施工的天数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OABC的顶点A在y轴正半轴上,顶点C在x轴正半轴上,抛物线
 (a<0)的顶点为D,且经过点A、B.若△ABD为等腰直角三角形,则a的值为___________.
(a<0)的顶点为D,且经过点A、B.若△ABD为等腰直角三角形,则a的值为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点A(-4,3),点B(-4,0),OA=5,以点O为直角顶点,点C在第一象限内,作等腰直角△AOC.
(1)直接写出点C坐标:
(2)直接写出四边形ABOC的面积:
(3)在y轴找一点P,使得△BOP的面积等于四边形ABOC的面积,请直接写出点P坐标:

相关试题

