搜索
【题目】如图，在平面直角坐标系中，正方形OABC的顶点A在y轴正半轴上，顶点C在x轴正半轴上，抛物线
（a<0）的顶点为D，且经过点A、B．若△ABD为等腰直角三角形，则a的值为___________．
参考答案：
【答案】-1
【解析】分析：抛物线
的对称轴方程为
即点
的横坐标为1，△ABD为等腰直角三角形，则点
的横坐标为2，正方形的边长为2，进而求出点的纵坐标为2+1=3，把点
代入抛物线解析式，即可求出
的值.
详解：抛物线的对称轴方程为
即点的横坐标为1，
△ABD为等腰直角三角形，则点的横坐标为2，正方形的边长为2，
,
代入抛物线解析式得：
解得：
故答案为：
点睛:属于二次函数综合体，考查待定系数法求函数解析式，正方形的性质，二次函数的图象与性质等，重点掌握待定系数法.
-
科目： 来源： 题型：
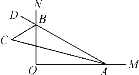
查看答案和解析>>【题目】如图，∠MON＝90°，点A，B分别在射线OM，ON上移动，∠OAB的平分线与∠OBA的外角平分线交于点C，试猜想：随着点A，B的移动，∠ACB的大小是否发生变化，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线
与坐标轴交于点
、
两点，直线
与直线
相交于点
，交
轴于点
，且
的面积为
.
(1)求
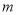的值和点的坐标；(2)求直线
的解析式；(3)若点
是线段上一动点，过点作
轴交直线于点
，
轴，
轴，垂足分别为点
、
，是否存在点，使得四边形
为正方形，若存在，请求出点
坐标，若不存在，请说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】长春市市政工程中需要铺设一条长660米的管道，为了尽量减少施工对城市交通造成的影响，实际施工时，每天铺设管道的长度比原计划增加10％，结果提前6天完成，求实际每天铺设管道的长度与实际施工天数．某同学根据题意列出方程
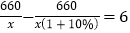，则方程中未知数x所表示的量是（ ）A. 原计划每天铺设管道的长度 B. 实际每天铺设管道的长度
C. 原计划施工的天数 D. 实际施工的天数
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，已知点A（-4，3），点B（-4，0）,OA=5,以点O为直角顶点，点C在第一象限内，作等腰直角△AOC.
（1）直接写出点C坐标：
（2）直接写出四边形ABOC的面积：
（3）在y轴找一点P,使得△BOP的面积等于四边形ABOC的面积，请直接写出点P坐标：
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙以50米/分的速度沿同一路线行走．设甲乙两人相距s（米），甲行走的时间为t（分），s关于t的函数图象的一部分如图所示．下列结论正确的个数是（ ）
（1）t＝5时，s＝150；（2）t＝35时，s＝450；（3）甲的速度是30米/分；（4）t＝12.5时，s＝0．
A. 1个B. 2个C. 3个D. 4个
-
科目： 来源： 题型：
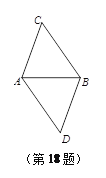
查看答案和解析>>【题目】如图，将线段AB绕点A逆时针旋转α度角得到线段AC，将线段AB绕点B逆时针旋转α度角得到线段BD（0°<α<180°），连结BC、AD．当α=_______度时，四边形ACBD是菱形，并说明理由．
相关试题
