Question

【题目】定义：如图1，抛物线 与 轴交于A，B两点，点P在抛物线上（点P与A，B两点不重合），如果△ABP的三边满足 ，则称点P为抛物线 的勾股点。

（1）直接写出抛物线 的勾股点的坐标；
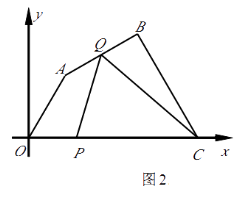
（2）如图2，已知抛物线C： 与 轴交于A，B两点，点P（1， ）是抛物线C的勾股点，求抛物线C的函数表达式；
（3）在（2）的条件下，点Q在抛物线C上，求满足条件 的点Q（异于点P）的坐标

Answer 1

【答案】
（1）

解：勾股点的坐标为（0，1）

（2）

解：抛物线y=ax2+bx（a≠0）过原点（0，0），即A（0，0），

如图作PG⊥x轴于点G，连接PA,PB，

∵点P（1，），

∴ AG=1,PG=,

∴PA=2,tan∠PAB=,

∴∠PAB=60°,
∴在Rt△PAB中，AB==4,

∴点B（4，0），

设y=ax（x-4）,当x=1时，y=,

解得a=-,

∴y=-x（x-4）=-x2+x.

（3）

解：① 当点Q在x轴上方，由S△ABQ=S△ABP,易知点Q的纵坐标为，

∴-x2+x=，解得x1=3,x2=1（不合题意，舍去），

∴Q（3，），

②当点Q在x轴下方，由S△ABQ=S△ABP,易知点Q的纵坐标为-，

∴-x2+x=-，解得x1=2+,x2=2-,

∴Q（2+，-）Q（2-，-），

综上，满足条件的点Q有三个：Q（3，）Q（2+，-）Q（2-，-）.

【解析】（1）解：y=-x2+1与x轴交于A（-1，0），B（1，0），与y轴交于P（0，1），
∴AB=2，AP=BP=,
∴AP2+BP2=AB2
∴勾股点P（0，1），