【题目】(阅读理解)
点A、B、C为数轴上三点,如果点C在A、B之间且到A的距离是点C到B的距离3倍,那么我们就称点C是{ A,B }的奇点.
例如,如图1,点A表示的数为﹣3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{ A,B }的奇点;又如,表示﹣2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B }的奇点,但点D是{B,A}的奇点.
(知识运用)
如图2,M、N为数轴上两点,点M所表示的数为﹣3,点N所表示的数为5.
(1)数 所表示的点是{ M,N}的奇点;数 所表示的点是{N,M}的奇点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣50,点B所表示的数为30.现有一动点P从点B出发向左运动,到达点A停止.P点运动到数轴上的什么位置时,P、A和B中恰有一个点为其余两点的奇点?
![]()
参考答案:
【答案】(1)3,-1 (2) -30, 10
【解析】
(1)根据定义发现:奇点表示的数到{M,N}中,前面的点M是到后面的数N的距离的3倍,从而得出结论;
根据定义发现:奇点表示的数到{N,M}中,前面的点N是到后面的数M的距离的3倍,从而得出结论;
(2)点A到点B的距离为6,由奇点的定义可知:分两种情况列式:①PB=3PA;②PA=3PB;可以得出结论.
(1)5-(-3)=8,
8÷(3+1)=2,
5-2=3,
-3+2=-1.
故表示数3的点是{M,N}的奇点;表示数-1的点是{N,M}的奇点.
(2)30-(-50)=80,
80÷(3+1)=20,
30-20=10,
-50+20=-30.
故点P运动到数轴上表示-30和10的点的位置时,P,A,B中恰有一个点为其余两点的奇点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列有理数大小关系判断正确的是( )
A. 0>|﹣10| B. ﹣(﹣
 )>﹣|﹣
)>﹣|﹣ | C. |﹣3|<|+3| D. ﹣1>﹣0.01
| C. |﹣3|<|+3| D. ﹣1>﹣0.01 -
科目: 来源: 题型:
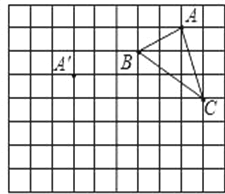
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,
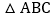 的三个顶点的位置如图所示,现将
的三个顶点的位置如图所示,现将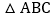 平移,使点A变换为点A′,点B′,C′,分别是B,C的对应点.
平移,使点A变换为点A′,点B′,C′,分别是B,C的对应点.(1)请画出平移后的
 ,并求
,并求 的面积;
的面积;(2)试说明△A'B'C'是如何由△ABC平移得到的;
(3)若连接AA′,CC′,则这两条线段之间的关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.

(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)A景区与C景区之间的距离是多少?
(3)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充足电而途中不充电的情况下完成此次任务?请计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣(﹣7)﹣(﹣5)+(﹣4)
(2)(﹣3
 )+12.5+(﹣16
)+12.5+(﹣16 )﹣(﹣2.5)
)﹣(﹣2.5)(3)(﹣24)×(
 )
) (4)18×(﹣
 )+13×
)+13× ﹣4×
﹣4×
(5)﹣12018 -
 ×[2×(﹣2)+10].
×[2×(﹣2)+10]. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)-5.4+0.2-0.6+1.8
(2) (-26.54)+(-6.4)+18.54+6.4
(3)

(4)

(5)

(6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图1,抛物线
 与
与  轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足
轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足  ,则称点P为抛物线
,则称点P为抛物线  的勾股点。
的勾股点。

(1)直接写出抛物线 的勾股点的坐标;
的勾股点的坐标;
(2)如图2,已知抛物线C: 与
与  轴交于A,B两点,点P(1,
轴交于A,B两点,点P(1,  )是抛物线C的勾股点,求抛物线C的函数表达式;
)是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件 的点Q(异于点P)的坐标
的点Q(异于点P)的坐标
相关试题

