搜索
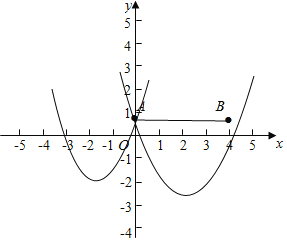
【题目】在平面直角坐标系xOy中，二次函数y＝x2﹣2mx+1图象与y轴的交点为A，将点A向右平移4个单位长度得到点B．
（1）直接写出点A与点B的坐标；
（2）求出抛物线的对称轴（用含m的式子表示）；
（3）若函数y＝x2﹣2mx+1的图象与线段AB恰有一个公共点，求m的取值范围．
参考答案：
【答案】（1）A（0，1），B（4，1）；（2）x＝m；（3）m≤0或m＞2．
【解析】
（1）计算自变量为0的函数值得到A点坐标，然后利用点平移的规律确定B点坐标；
（2）利用抛物线的对称轴方程求解；
（3）当对称轴为y轴时，满足条件，此时m＝0；当m＜0时满足条件；若m＞0时，利用当x＝4，y＜1时抛物线与线段AB恰有一个公共点，然后求出此时m的范围．
解：（1）当x＝0时，y＝x2﹣2mx+1＝1，则A点坐标为（0，1），
把A（0，1）右平移4个单位长度得到点B，则B点坐标为（4，1），
（2）抛物线的对称轴为直线x＝-
＝m；
（3）当m＝0时，抛物线解析式为y＝x2+1，此抛物线与线段AB恰有一个公共点；
当m＜0时，抛物线与线段AB恰有一个公共点；
当m＞0时，当x＝4，y＜1，即16﹣8m+1＜1，解得m＞2，
所以m的范围为m≤0或m＞2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，反比例函数y＝
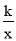（x＞0）的图象G与直线l：y＝2x﹣4交于点A（3，a）．（1）求k的值；
（2）已知点P（0，n）（n＞0），过点P作平行于x轴的直线，与图象G交于点B，与直线l交于点C．横、纵坐标都是整数的点叫做整点．记图象G在点A，B之间的部分与线段AC，BC围成的区域（不含边界）为W．
①当n＝5时，直接写出区域W内的整点个数；
②若区域W内的整点恰好为3个，结合函数图象，直接写出n的取值范围．
-
科目： 来源： 题型：
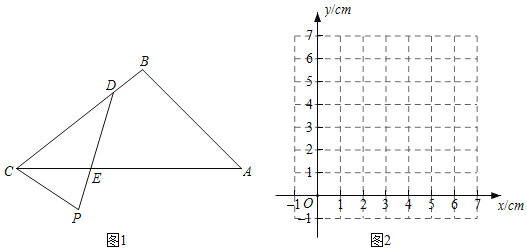
查看答案和解析>>【题目】如图1，P是△ABC外部的一定点，D是线段BC上一动点，连接PD交AC于点E．
小明根据学习函数的经验，对线段PD，PE，CD的长度之间的关系进行了探究，
下面是小明的探究过程，请补充完整：
（1）对于点D在BC上的不同位置，画图、测量，得到了线段PD，PE，CD的长度的几组值，如表：
位置1
位置2
位置3
位置4
位置5
位置6
位置7
位置8
位置9
PD/cm
2.56
2.43
2.38
2.43
2.67
3.16
3.54
4.45
5.61
PE/cm
2.56
2.01
1.67
1.47
1.34
1.32
1.34
1.40
1.48
CD/cm
0.00
0.45
0.93
1.40
2.11
3.00
3.54
4.68
6.00
在PD，PE，CD的长度这三个量中，确定 的长度是自变量， 的长度和 的长度都是这个自变量的函数；
（2）在同一平面直角坐标系xOy中，画出图2中所确定的两个函数的图象；
（3）结合函数图象，解决问题：
连接CP，当△PCD为等腰三角形时，CD的长度约为 cm．（精确到0.1）
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC中，AB＝BC，∠ABC＝90°，将线段AB绕点A逆时针旋转α（0°＜α＜90°）得到线段AD．作射线BD，点C关于射线BD的对称点为点E．连接AE，CE．
（1）依题意补全图形；
（2）若α＝20°，直接写出∠AEC的度数；
（3）写出一个α的值，使AE＝
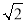时，线段CE的长为
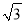﹣1，并证明．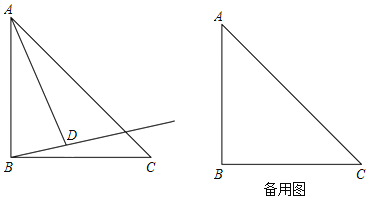
-
科目： 来源： 题型：
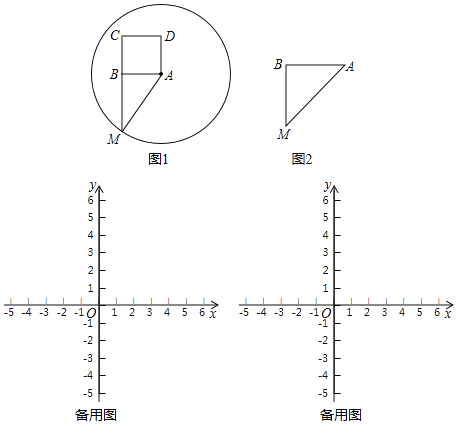
查看答案和解析>>【题目】在△ABM中，∠ABM＝90°，以AB为一边向△ABM的异侧作正方形ABCD，以A为圆心，AM为半径作⊙A，我们称正方形ABCD为⊙A的“关于△ABM的友好正方形”，如果正方形ABCD恰好落在⊙A的内部（或圆上），我们称正方形ABCD为⊙A的“关于△ABM的绝对友好正方形”，例如，图1中正方形ABCD是⊙A的“关于△ABM的友好正方形”．
（1）图2中，△ABM中，BA＝BM，∠ABM＝90°，在图中画出⊙A的“关于△ABM的友好正方形ABCD”．
（2）若点A在反比例函数y＝
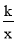（k＞0，x＞0）上，它的横坐标是2，过点A作AB⊥y轴于B，若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”，求k的取值范围．（3）若点A是直线y＝﹣x+2上的一个动点，过点A作AB⊥y轴于B，若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”，求出点A的横坐标m的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示的网格是正方形网格，则∠PAB﹣∠PCD＝_____°．（点A，B，C，D，P是网格线交点）
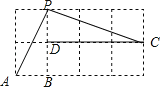
相关试题
