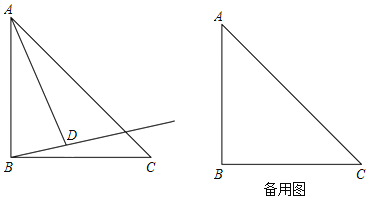
【题目】△ABC中,AB=BC,∠ABC=90°,将线段AB绕点A逆时针旋转α(0°<α<90°)得到线段AD.作射线BD,点C关于射线BD的对称点为点E.连接AE,CE.
(1)依题意补全图形;
(2)若α=20°,直接写出∠AEC的度数;
(3)写出一个α的值,使AE=![]() 时,线段CE的长为
时,线段CE的长为![]() ﹣1,并证明.
﹣1,并证明.
参考答案:
【答案】(1)见解析;(2)∠AEC=135°;(3)α=30°,证明见解析
【解析】
(1)作CF⊥BD并延长CF到E使EF=CF,如图1,
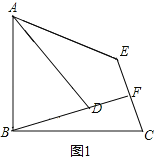
(2)连结BE,如图2,利用对称的性质得BE=BC,则BC=BE=BA,则根据等腰三角形的性质得出∠BCE=∠BEC,∠BAE=∠BEA,由四边形的内角和可计算出∠BCE+∠BEC+∠BAE+∠BEA+∠ABC=360°,进而得到2(∠BEC+∠BEA)=270°,即可证得∠BEC+∠BEA=135°,即∠AEC=135°;
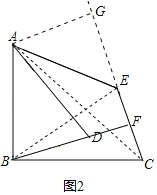
(3)如图2,先证明△AGE为等腰直角三角形,则AG=GE=1,当α=30°时,则∠EBC=30°,进而求得∠ACG=30°,解直角三角形求得CG=![]() ,即可证得CE=CG﹣EG=
,即可证得CE=CG﹣EG=![]() ﹣1.
﹣1.
解:(1)如图1,
(2)∠AEC=135°,
证明:过A作AG⊥CE于G.连接AC、BE,如图2,
由题意,BC=BE=BA,
∴∠BCE=∠BEC,∠BAE=∠BEA,
∵∠BCE+∠BEC+∠BAE+∠BEA+∠ABC=360°
∵∠ABC=90°,
∴2(∠BEC+∠BEA)=270°,
∴∠BEC+∠BEA=135°,即∠AEC=135°,
(3)α=30°,
证明:∵∠AEC=135°,
∴∠AEG=45°,
∵AE=![]() ,
,
∴AG=GE=1,
当α=30°时,
∴∠EBC=30°,
∵BC=BE,
∴∠BCG=75°,
∵∠BCA=45°,
∴∠ACG=30°,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,P是△ABC外部的一定点,D是线段BC上一动点,连接PD交AC于点E.
小明根据学习函数的经验,对线段PD,PE,CD的长度之间的关系进行了探究,
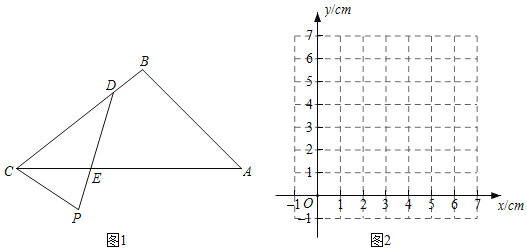
下面是小明的探究过程,请补充完整:
(1)对于点D在BC上的不同位置,画图、测量,得到了线段PD,PE,CD的长度的几组值,如表:
位置1
位置2
位置3
位置4
位置5
位置6
位置7
位置8
位置9
PD/cm
2.56
2.43
2.38
2.43
2.67
3.16
3.54
4.45
5.61
PE/cm
2.56
2.01
1.67
1.47
1.34
1.32
1.34
1.40
1.48
CD/cm
0.00
0.45
0.93
1.40
2.11
3.00
3.54
4.68
6.00
在PD,PE,CD的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出图2中所确定的两个函数的图象;
(3)结合函数图象,解决问题:
连接CP,当△PCD为等腰三角形时,CD的长度约为 cm.(精确到0.1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,二次函数y=x2﹣2mx+1图象与y轴的交点为A,将点A向右平移4个单位长度得到点B.
(1)直接写出点A与点B的坐标;
(2)求出抛物线的对称轴(用含m的式子表示);
(3)若函数y=x2﹣2mx+1的图象与线段AB恰有一个公共点,求m的取值范围.
-
科目: 来源: 题型:
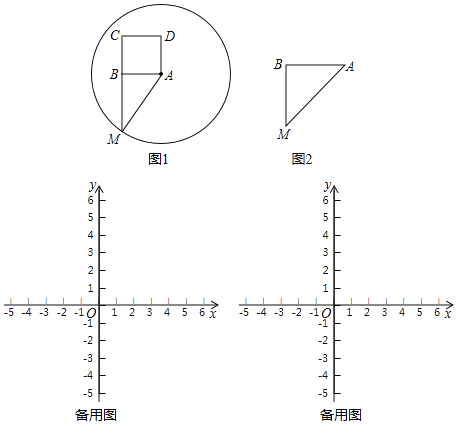
查看答案和解析>>【题目】在△ABM中,∠ABM=90°,以AB为一边向△ABM的异侧作正方形ABCD,以A为圆心,AM为半径作⊙A,我们称正方形ABCD为⊙A的“关于△ABM的友好正方形”,如果正方形ABCD恰好落在⊙A的内部(或圆上),我们称正方形ABCD为⊙A的“关于△ABM的绝对友好正方形”,例如,图1中正方形ABCD是⊙A的“关于△ABM的友好正方形”.
(1)图2中,△ABM中,BA=BM,∠ABM=90°,在图中画出⊙A的“关于△ABM的友好正方形ABCD”.
(2)若点A在反比例函数y=
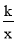 (k>0,x>0)上,它的横坐标是2,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求k的取值范围.
(k>0,x>0)上,它的横坐标是2,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求k的取值范围.(3)若点A是直线y=﹣x+2上的一个动点,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求出点A的横坐标m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的网格是正方形网格,则∠PAB﹣∠PCD=_____°.(点A,B,C,D,P是网格线交点)
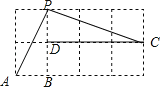
-
科目: 来源: 题型:
查看答案和解析>>【题目】明代的程大位创作了《算法统宗》,它是一本通俗实用的数学书,将枯燥的数学问题化成了美妙的诗歌,读来朗朗上口,是将数字入诗的代表作.其中有一首饮酒数学诗:“肆中饮客乱纷纷,薄酒名醨厚酒醇.醇酒一瓶醉三客,薄酒三瓶醉一人,共同饮了一十九,三十三客醉颜生,试问高明能算士,几多醨酒几多醇?”这首诗是说:“好酒一瓶,可以醉倒3位客人;薄酒三瓶,可以醉倒1位客人,如今33位客人醉倒了,他们总共饮下19瓶酒.试问:其中好酒、薄酒分别是多少瓶?”设有好酒x瓶,薄酒y瓶.根据题意,可列方程组为_____.
相关试题

