【题目】如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,连接AF、BE交于点G,连接CE、DF交于点H.
(1)求证:四边形EGFH为平行四边形;
(2)当![]() = 时,四边形EGFH为矩形。
= 时,四边形EGFH为矩形。

参考答案:
【答案】(1)见解析;
(2)当![]() 时,平行四边形EGFH是矩形,理由见解析.
时,平行四边形EGFH是矩形,理由见解析.
【解析】
(1)可分别证明四边形AFCE是平行四边形,四边形BFDE是平行四边形,从而得出GF∥EH,GE∥FH,即可证明四边形EGFH是平行四边形.
(2)证出四边形ABFE是菱形,得出AF⊥BE,即∠EGF=90°,即可得出结论.
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵点E. F分别是AD、BC的中点
∴AE=ED=![]() AD,BF=FC=
AD,BF=FC=![]() BC,
BC,
∴AE∥FC,AE=FC.
∴四边形AECF是平行四边形.
∴GF∥EH.
同理可证:ED∥BF且ED=BF.
∴四边形BFDE是平行四边形.
∴GE∥FH.
∴四边形EGFH是平行四边形.
(2)当![]() 时,平行四边形EGFH是矩形.理由如下:
时,平行四边形EGFH是矩形.理由如下:
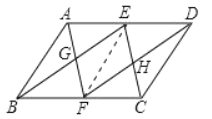
连接EF,如图所示:
由(1)同理可证四边形ABFE是平行四边形,
当![]() 时,即BC=2AB,AB=BF,
时,即BC=2AB,AB=BF,
∴四边形ABFE是菱形,
∴AF⊥BE,即∠EGF=90,
∴平行四边形EGFH是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
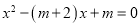 (m为常数)
(m为常数)(1)求证:不论m为何值,方程总有两个不相等的实数根;
(2)若方程有一个根是2,求m的值及方程的另一个根。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣8,点C 在数轴上表示的数是10.若线段AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度也向右匀速运动.

(1)运动t秒后,点B表示的数是 ;点C表示的数是 .(用含有t的代数式表示)
(2)求运动多少秒后,BC=4(单位长度);
(3)P是线段AB上一点,当B点运动到线段CD上时,是否存在关系式
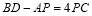 ,若存在,求线段PD的长;若不存在,请说明理由.
,若存在,求线段PD的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在下列说法中 ①0.09是0.81的平方根;②-9的平方根是±3;③
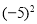 的算术平方根是-5;④
的算术平方根是-5;④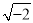 是一个负数;⑤0的相反数和倒数都是0;⑥
是一个负数;⑤0的相反数和倒数都是0;⑥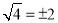 ;⑦如果一个数的立方根是这个数的本身,那么这个数是1或0;⑧全体实数和数轴上的点一一对应.正确的有_________.
;⑦如果一个数的立方根是这个数的本身,那么这个数是1或0;⑧全体实数和数轴上的点一一对应.正确的有_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】老师在黑板上出了一道解方程的题:
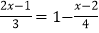 ,小明马上举起了手,要求到黑板上去做,他是这样做的:4(2x﹣1)=1﹣3(x+2),①
,小明马上举起了手,要求到黑板上去做,他是这样做的:4(2x﹣1)=1﹣3(x+2),①8x﹣4=1﹣3x﹣6,②
8x+3x=1﹣6+4,③
11x=﹣1,④
x=﹣
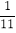 .⑤
.⑤老师说:小明解一元一次方程的一般步骤都掌握了,但解题时有一步做错了.请你指出他错在第 步(填编号),然后再细心地解下面的方程,相信你一定能做对.
(1)5(x+8)=6(2x﹣7)+5;
(2)
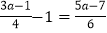 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数
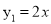 与反比例函数
与反比例函数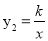 的图像交于A,B两点,过点A作AC⊥x轴,垂足为C,△ACO的面积为4。
的图像交于A,B两点,过点A作AC⊥x轴,垂足为C,△ACO的面积为4。(1)求反比例函数的表达式;
(2)点B的坐标为 ;
(3)当
 时,直接写出x的取值范围。
时,直接写出x的取值范围。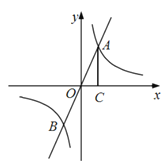
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级共有800名学生,准备调查他们对“低碳”知识的了解程度.
(1)在确定调查方式时,团委设计了以下三种方案:
方案一:调查七年级部分女生;
方案二:调查七年级部分男生;
方案三:到七年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是 ;
(2)团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示),请你根据图中信息,将两个统计图补充完整;

(3)在扇形统计图中,“比较了解”所在扇形的圆心角的度数是 .
(4)请你估计该校七年级约有 名学生比较了解“低碳”知识.
相关试题

