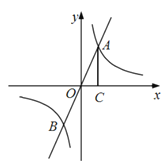
【题目】如图,正比例函数![]() 与反比例函数
与反比例函数![]() 的图像交于A,B两点,过点A作AC⊥x轴,垂足为C,△ACO的面积为4。
的图像交于A,B两点,过点A作AC⊥x轴,垂足为C,△ACO的面积为4。
(1)求反比例函数的表达式;
(2)点B的坐标为 ;
(3)当![]() 时,直接写出x的取值范围。
时,直接写出x的取值范围。
参考答案:
【答案】解: ![]() ;
;
(2)B(-2,-4);
(3)-2<x<0或x>2.
【解析】
(1)根据反比例函数图象的性质,反比例函数上任意一点向x轴(或y轴)作垂线,这一点、所交点与原点之间所围成的直角三角形的面积等于![]() ,图象经过一、三象限k>0;
,图象经过一、三象限k>0;
(2)联立正比例函数与反比例函数,解出的x,y分别为交点的横、纵坐标,这里需注意解得的解集有两个,说明交点有两个,需要考虑点所在位于哪一个象限;
(3)观察图像可以解决问题,谁的图像在上面,谁对应的函数值大,这里需过两个交点作x轴垂线,两条垂线与y轴将图象分成四部分,分别讨论.
解:(1)∵△ACO的面积为4,C⊥x轴
∴![]() ,
,
即![]() ,
,
∵点A是函数![]() 的点
的点
∴![]() ,
,
∵反比例函数的图像在第一、三象限,
∴k>0
∴k=8,反比例函数表达式为![]() ;
;
(2)联立 ,可解得
,可解得![]() 或
或![]() ,
,
∵B点在第三象限,
∴点B坐标为(-2,-4).
(3)根据(2)易得A点坐标为(2,4),
所以当-2<x<0或x>2时,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列说法中 ①0.09是0.81的平方根;②-9的平方根是±3;③
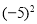 的算术平方根是-5;④
的算术平方根是-5;④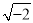 是一个负数;⑤0的相反数和倒数都是0;⑥
是一个负数;⑤0的相反数和倒数都是0;⑥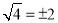 ;⑦如果一个数的立方根是这个数的本身,那么这个数是1或0;⑧全体实数和数轴上的点一一对应.正确的有_________.
;⑦如果一个数的立方根是这个数的本身,那么这个数是1或0;⑧全体实数和数轴上的点一一对应.正确的有_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,连接AF、BE交于点G,连接CE、DF交于点H.
(1)求证:四边形EGFH为平行四边形;
(2)当
 = 时,四边形EGFH为矩形。
= 时,四边形EGFH为矩形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师在黑板上出了一道解方程的题:
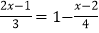 ,小明马上举起了手,要求到黑板上去做,他是这样做的:4(2x﹣1)=1﹣3(x+2),①
,小明马上举起了手,要求到黑板上去做,他是这样做的:4(2x﹣1)=1﹣3(x+2),①8x﹣4=1﹣3x﹣6,②
8x+3x=1﹣6+4,③
11x=﹣1,④
x=﹣
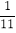 .⑤
.⑤老师说:小明解一元一次方程的一般步骤都掌握了,但解题时有一步做错了.请你指出他错在第 步(填编号),然后再细心地解下面的方程,相信你一定能做对.
(1)5(x+8)=6(2x﹣7)+5;
(2)
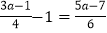 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级共有800名学生,准备调查他们对“低碳”知识的了解程度.
(1)在确定调查方式时,团委设计了以下三种方案:
方案一:调查七年级部分女生;
方案二:调查七年级部分男生;
方案三:到七年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是 ;
(2)团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示),请你根据图中信息,将两个统计图补充完整;

(3)在扇形统计图中,“比较了解”所在扇形的圆心角的度数是 .
(4)请你估计该校七年级约有 名学生比较了解“低碳”知识.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:在分式中,对于只含有一个字母的分式,当分子的次数小于分母的次数时,我们称之为“真分式”,如:
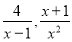 。当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如:
。当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如: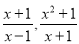 。假分式可以化为整式与真分式和的形式,我们也称之为带分式,如:
。假分式可以化为整式与真分式和的形式,我们也称之为带分式,如: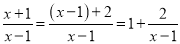 。
。解决问题:
(1)下列分式中属于真分式的是( )
A.
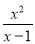 B.
B.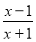 C.
C.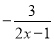 D.
D.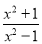
(2)将假分式
 分别化为带分式;
分别化为带分式;(3)若假分式
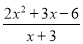 的值为整数,请直接写出所有符合条件的整数x的值。
的值为整数,请直接写出所有符合条件的整数x的值。 -
科目: 来源: 题型:
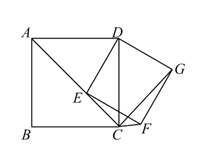
查看答案和解析>>【题目】如图,已知四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG。
(1)求证:矩形DEFG是正方形。
(2)当点E从A点运动到C点时;
①求证:∠DCG的大小始终不变;
②若正方形ABCD的边长为2,则点G运动的路径长为 。
相关试题

