【题目】已知关于x的一元二次方程![]() (m为常数)
(m为常数)
(1)求证:不论m为何值,方程总有两个不相等的实数根;
(2)若方程有一个根是2,求m的值及方程的另一个根。
参考答案:
【答案】(1)见解析;
(2) 即m的值为0,方程的另一个根为0.
【解析】
(1)可用根的判别式,计算判别式得到△=(m+2)24×1m=m2+4>0,则方程有两个不相等实数解,于是可判断不论m为何值,方程总有两个不相等的实数根;
(2)设方程的另一个根为t,利用根与系数的关系得到2+t=![]() ,2t=m,最终解出关于t和m的方程组即可.
,2t=m,最终解出关于t和m的方程组即可.
(1)证明:
△=(m+2)24×1m=m2+4,
∵无论m为何值时m2≥0,
∴m2+4≥4>0,
即△>0,
所以无论m为何值,方程总有两个不相等的实数根.
(2)设方程的另一个根为t,
![]()
根据题意得2+t=![]() ,2t=m,
,2t=m,
解得t=0,
所以m=0,
即m的值为0,方程的另一个根为0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A,B两点分别在x轴,y轴的正半轴上,且OA=OB,点C在第一象限,OC=3,连接BC,AC,若∠BCA=90°,则BC+AC的值为_________。
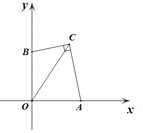
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=
 的图象分别交于C、D两点,点D的坐标为(2,-3),点B是线段AD的中点.则不等式 k1x+b —
的图象分别交于C、D两点,点D的坐标为(2,-3),点B是线段AD的中点.则不等式 k1x+b — >0的解集是___________.
>0的解集是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一只不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,然后把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
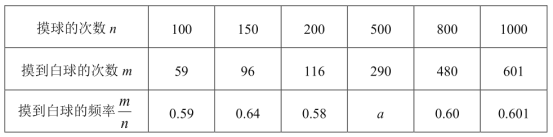
(1)上表中的a= ;
(2)“摸到白球”的概率的估计值是 (精确到0.1)
(3)试估算口袋中黑、白两种颜色的球各有多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣8,点C 在数轴上表示的数是10.若线段AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度也向右匀速运动.

(1)运动t秒后,点B表示的数是 ;点C表示的数是 .(用含有t的代数式表示)
(2)求运动多少秒后,BC=4(单位长度);
(3)P是线段AB上一点,当B点运动到线段CD上时,是否存在关系式
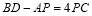 ,若存在,求线段PD的长;若不存在,请说明理由.
,若存在,求线段PD的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在下列说法中 ①0.09是0.81的平方根;②-9的平方根是±3;③
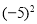 的算术平方根是-5;④
的算术平方根是-5;④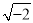 是一个负数;⑤0的相反数和倒数都是0;⑥
是一个负数;⑤0的相反数和倒数都是0;⑥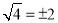 ;⑦如果一个数的立方根是这个数的本身,那么这个数是1或0;⑧全体实数和数轴上的点一一对应.正确的有_________.
;⑦如果一个数的立方根是这个数的本身,那么这个数是1或0;⑧全体实数和数轴上的点一一对应.正确的有_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,连接AF、BE交于点G,连接CE、DF交于点H.
(1)求证:四边形EGFH为平行四边形;
(2)当
 = 时,四边形EGFH为矩形。
= 时,四边形EGFH为矩形。
相关试题

