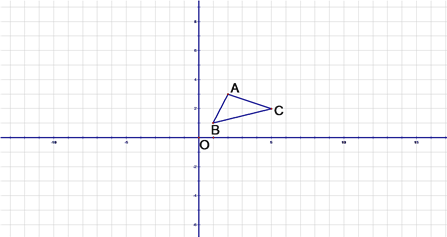
【题目】如图,A(2,3),B(1,1),C(5,2)以原点O为位似中心,相似比为2, 将△ABC进行变换,画出变换后的图形,并求出相应的坐标.
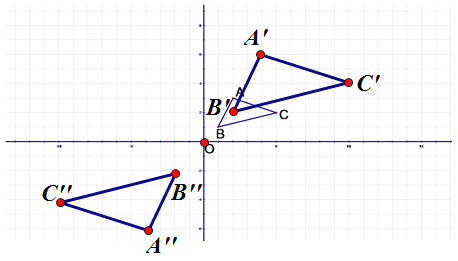
参考答案:
【答案】图形见解析
【解析】若位似比是k,则原图形上的点(x,y),经过位似变化得到的对应点的坐标是(kx,ky)或(-kx,-ky),即可得出A、B、C的对应点的坐标,顺序连接各点即可画出变换出的图形.
解:∵A(2,3)以原点O为位似中心,相似比为2,将△ABC放大,
∴A的对应点的坐标是(4,6)或(4,6) ,
B的对应点的坐标是(2,2)或(2,2) ,
C的对应点的坐标是(10,4)或(10,4) ,
同理,点A、B、C位似变换后的对应点的坐标(4,6),(2,2),(10,4)或(4,6),(2,2),(10,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,每个小方格都是边长为
 的正方形,
的正方形, 的顶点均在格点上,点
的顶点均在格点上,点 的坐标是
的坐标是 .
.
(1)将
 先向右平移
先向右平移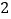 个单位长度,再向下平移
个单位长度,再向下平移 个单位长度,在图中画出第二次平移后的图形△
个单位长度,在图中画出第二次平移后的图形△ .
.(2)如果将
 看成是由
看成是由 经过一次平移得到的,则这一次平移的方向为_________,平移的距离为___________.
经过一次平移得到的,则这一次平移的方向为_________,平移的距离为___________.(3)请画出
 关于坐标原点
关于坐标原点 的中心对称图形
的中心对称图形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处M(点M在DE上)距D点3米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在某月的日历上,圈出
 ,
, ,
, ,
, ,
, ,5个数,使它们呈一个十字架.
,5个数,使它们呈一个十字架.
(1)如果它的和为55,求
 的值;
的值;(2)如果它们的和为115,求D的值;
(3)这五个数的和可以是125吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第1个
 中,
中, 40°,
40°, ,在
,在 上取一点
上取一点 ,延长
,延长 到
到 ,使得在第2个
,使得在第2个 中,
中, ;在
;在 上取一点
上取一点 ,延长
,延长 到
到 ,使得在第3个
,使得在第3个 中,
中, ;…,按此做法进行下去,第3个三角形中以
;…,按此做法进行下去,第3个三角形中以 为顶点的内角的度数为_____; 第
为顶点的内角的度数为_____; 第 个三角形中以
个三角形中以 为顶点的内角的度数为_____度.
为顶点的内角的度数为_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式:①
 ;②
;② ;③
;③ .
.(1)根据你观察、归纳、发现的规律,写出
 可以是______的平方.
可以是______的平方.(2)试猜想写出第
 个等式,并说明成立的理由.
个等式,并说明成立的理由.(3)利用前面的规律,将
 改成完全平方的形式为:______.
改成完全平方的形式为:______.
相关试题

