【题目】如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处M(点M在DE上)距D点3米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?

参考答案:
【答案】解:(1)能看到,理由如下:
由题意得,∠DFG=90°﹣53°=37°,则![]() =tan∠DFG。
=tan∠DFG。
∵DF=4米,∴DG=4×tan37°=4×0.75=3(米)。
∵老鼠躲藏处M(点M在DE上)距D点3米,∴猫头鹰能看到这只老鼠。
(2)由(1)得,AG=AD+DG=2.7+3=5.7(米),
又![]() =sin∠C=sin37°,则CG=
=sin∠C=sin37°,则CG=![]() (米)。
(米)。
答:要捕捉到这只老鼠,猫头鹰至少要飞9.5米。
【解析】试题分析:(1)根据猫头鹰从C点观测F点的俯角为53°,可知∠DFG=90°﹣53°=37°,在△DFG中,已知DF的长度,求出DG的长度,若DG>3,则看不见老鼠,若DG<3,则可以看见老鼠。
(2)根据(1)求出的DG长度,求出AG的长度,然后在Rt△CAG中,根据![]() =sin∠C=sin37°,即可求出CG的长度。
=sin∠C=sin37°,即可求出CG的长度。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:-3x3·(5x2-1)=____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(-2x2)3·(x2+x2y2+y2)的结果中次数是10的项的系数是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解八年级学生参加社会实践活动情况,某区教育部门随机调查了本区部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
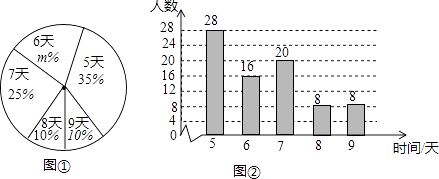
(1)本次接受随机抽样调查的学生人数为 , 图①中的m的值为;
(2)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(3)若该区八年级学生有3000人,估计参加社会实践活动时间大于7天的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合, OD与BC交于点E,设点D的坐标是
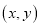 ,则
,则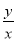 的值为( )
的值为( )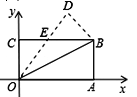
A.
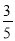 B.
B. 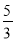 C.
C. 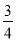 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形OABC的两个顶点A、B 的坐标分别A(
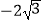 ,0)、B(
,0)、B( 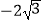 ,2),∠CAO=30°.
,2),∠CAO=30°.
(1)求对角线AC所在的直线的函数表达式;
(2)把矩形OABC以AC所在的直线为对称轴翻折,点O落在平面上的点D处,求点D的坐标;
(3)在平面内是否存在点P,使得以A、O、D、P为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
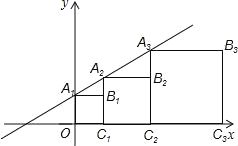
查看答案和解析>>【题目】在平面直角坐标系xOy中,记直线y=x+1为l.点A1是直线l与y轴的交点,以A1O为边作正方形A1OC1B1,使点C1落在在x轴正半轴上,作射线C1B1交直线l于点A2,以A2C1为边作正方形A2C1C2B2,使点C2落在在x轴正半轴上,依次作下去,得到如图所示的图形.则点B4的坐标是 ,点Bn的坐标是 .
相关试题

