【题目】观察下列各式:①![]() ;②
;②![]() ;③
;③![]() .
.
(1)根据你观察、归纳、发现的规律,写出![]() 可以是______的平方.
可以是______的平方.
(2)试猜想写出第![]() 个等式,并说明成立的理由.
个等式,并说明成立的理由.
(3)利用前面的规律,将![]() 改成完全平方的形式为:______.
改成完全平方的形式为:______.
参考答案:
【答案】(1)4025;(2)![]() ,见解析;(3)
,见解析;(3)![]() .
.
【解析】
(1)根据已知的三个等式,发现规律:等式左边是序号数与比序号数大1的两个正整数积的4倍与1的和,等式右边是序号数与比序号数大1的两个正整数的和的平方,由此得出4×2012×2013+1可以看成2012与2013这两个正整数的和的平方;
(2)猜想第n个等式为4n(n+1)+1=(n+n+1)![]() =(2n+1)
=(2n+1)![]() ,运用多项式的乘法法则计算验证即可;
,运用多项式的乘法法则计算验证即可;
(3)利用前面的规律,可知![]() =
=![]()
(1)根据观察、归纳、发现的规律,得到4×2012×2013+1=(2012+2013)![]() =4025
=4025![]() ;
;
(2)猜想第n个等式为4n(n+1)+1=(2n+1)![]() ,理由如下:
,理由如下:
∵左边=4n(n+1)+1=4n![]() +4n+1,右边=(2n+1)
+4n+1,右边=(2n+1)![]() =4n
=4n![]() +4n+1,
+4n+1,
∴左边=右边,
∴4n(n+1)+1=(2n+1)![]() ;
;
(3)利用前面的规律,可知
![]() 即
即![]()
-
科目: 来源: 题型:
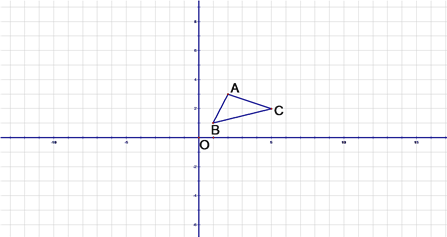
查看答案和解析>>【题目】如图,A(2,3),B(1,1),C(5,2)以原点O为位似中心,相似比为2, 将△ABC进行变换,画出变换后的图形,并求出相应的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在某月的日历上,圈出
 ,
, ,
, ,
, ,
, ,5个数,使它们呈一个十字架.
,5个数,使它们呈一个十字架.
(1)如果它的和为55,求
 的值;
的值;(2)如果它们的和为115,求D的值;
(3)这五个数的和可以是125吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第1个
 中,
中, 40°,
40°, ,在
,在 上取一点
上取一点 ,延长
,延长 到
到 ,使得在第2个
,使得在第2个 中,
中, ;在
;在 上取一点
上取一点 ,延长
,延长 到
到 ,使得在第3个
,使得在第3个 中,
中, ;…,按此做法进行下去,第3个三角形中以
;…,按此做法进行下去,第3个三角形中以 为顶点的内角的度数为_____; 第
为顶点的内角的度数为_____; 第 个三角形中以
个三角形中以 为顶点的内角的度数为_____度.
为顶点的内角的度数为_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大学公益组织计划购买
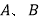 两种的文具套装进行捐赠,关注留守儿童经洽谈,购买
两种的文具套装进行捐赠,关注留守儿童经洽谈,购买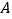 套装比购买
套装比购买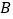 套装多用20元,且购买5套
套装多用20元,且购买5套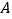 套装和4套
套装和4套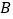 套装共需820元.
套装共需820元.(1)求购买一套
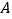 套装文具、一套
套装文具、一套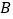 套装各需要多少元?
套装各需要多少元?(2)根据该公益组织的募捐情况和捐助对象情况,需购买
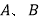 两种套装共60套,要求购买
两种套装共60套,要求购买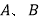 两种套装的总费用不超过5240元,则购买
两种套装的总费用不超过5240元,则购买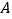 套装最多多少套?
套装最多多少套? -
科目: 来源: 题型:
查看答案和解析>>【题目】探究与发现:
如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这种图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?请解决以下问题:
(1)观察“规形图”,试探究∠BPC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下问题:
①如图2:已知△ABC,BP平分∠ABC,CP平分∠ACB,直接写出∠BPC与∠A之间存在的等量关系为: .
迁移运用:如图3:在△ABC中,∠A=80°,点O是∠ABC,∠ACB角平分线的交点,点P是∠BOC,∠OCB角平分线的交点,若∠OPC=100°,则∠ACB的度数 .
②如图4:若D点是△ABC内任意一点,BP平分∠ABD,CP平分∠ACD.直接写出∠BDC、∠BPC、∠A之间存在的等量关系为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】养牛场原有大牛30头和小牛15头,一天约用饲料675kg.一周后又购进12头大牛和5头小牛,这时1天约用饲料940kg.饲养员李大叔估计每头大牛1天约需饲料1820kg,每头小牛1天约需饲料78kg,你能通过计算检验他的估计吗?
相关试题

