【题目】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
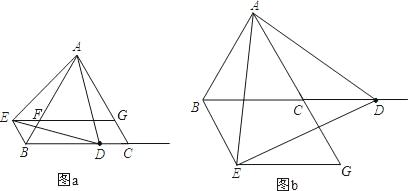
(1)如图(a)所示,当点D在线段BC上时.
①求证:△AEB≌△ADC;
②探究四边形BCGE是怎样特殊的四边形?并说明理由;
(2)如图(b)所示,当点D在BC的延长线上时,直接写出(1)中的两个结论是否成立;
(3)在(2)的情况下,当点D运动到什么位置时,四边形BCGE是菱形?并说明理由.
参考答案:
【答案】(1)①见解析,②四边形BCGE是平行四边形,见解析;(2)①②都成立;(3)当CD=CB (∠CAD=30°或∠BAD=90°或∠ADC=30°)时,四边形BCGE是菱形,见解析.
【解析】
(1)根据等边三角形的性质可得AB=AC,AE=AD,∠BAC=∠EAD=60°,然后求出∠BAE=∠CAD,再利用“边角边”证明△AEB和△ADC全等;②四边形BCGE是平行四边形,因为△AEB≌△ADC,所以可得∠ABE=∠C=60°,进而证明∠ABE=∠BAC,则可得到EB∥GC又EG∥BC,所以四边形BCGE是平行四边形;
(2)根据(1)的思路解答即可.(3)当CD=CB时,四边形BCGE是菱形,由(1)可知△AEB≌△ADC,可得BE=CD,再证明BE=CB,即邻边相等的平行四边形是菱形.
证明:(1)①∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°.
又∵∠EAB=∠EAD﹣∠BAD,∠DAC=∠BAC﹣∠BAD,
∴∠EAB=∠DAC,
∴△AEB≌△ADC(SAS).
②方法一:由①得△AEB≌△ADC,
∴∠ABE=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABE=∠BAC,
∴EB∥GC.
又∵EG∥BC,
∴四边形BCGE是平行四边形.
方法二:证出△AEG≌△ADB,得EG=AB=BC.
∵EG∥BC,
∴四边形BCGE是平行四边形.
(2)①②都成立.
(3)当CD=CB (∠CAD=30°或∠BAD=90°或∠ADC=30°)时,四边形BCGE是菱形.
理由:方法一:由①得△AEB≌△ADC,
∴BE=CD
又∵CD=CB,
∴BE=CB.
由②得四边形BCGE是平行四边形,
∴四边形BCGE是菱形.
方法二:由①得△AEB≌△ADC,
∴BE=CD.
又∵四边形BCGE是菱形,
∴BE=CB
∴CD=CB.
方法三:∵四边形BCGE是平行四边形,
∴BE∥CG,EG∥BC,
∴∠FBE=∠BAC=60°,∠F=∠ABC=60°
∴∠F=∠FBE=60°,∴△BEF是等边三角形.
又∵AB=BC,四边形BCGE是菱形,
∴AB=BE=BF,
∴AE⊥FG
∴∠EAG=30°,
∵∠EAD=60°,
∴∠CAD=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张老师抽取了九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,规定x≥6.25为合格,x≥9.25为优秀.并绘制出扇形统计图和频数分布直方图(不完整).
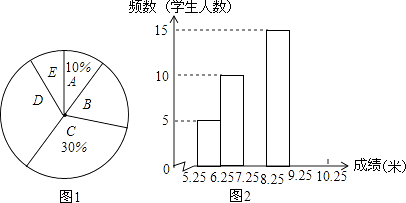
(1)抽取的这部分男生有人,请补全频数分布直方图;
(2)抽取的这部分男生成绩的中位数落在组?扇形统计图中D组对应的圆心角是多少度?
(3)如果九年级有男生400人,请你估计他们掷实心球的成绩达到合格的有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
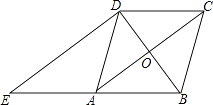
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△A'B'C',点C的对应点是直线上的格点C'.
(1)画出△A'B'C';
(2)在BC上找一点P,使AP平分△ABC的面积;
(3)试在直线l上画出所有的格点Q,使得由点A'、B'、C'、Q四点围成的四边形的面积为9.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小林是三河中学九年级的同班同学,在四月份举行的自主招生考试中,他俩都被同一所高中提前录取,并将被编入A,B,C三个班,他俩希望能再次成为同班同学.
(1)请你用画树状图法或列举法,列出所有可能的结果;
(2)求两人再次成为同班同学的概率. -
科目: 来源: 题型:
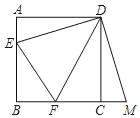
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D按逆时针方向旋转90°得到△DCM.
(1)求证:EF=MF;(2)当AE=1时,求EF的长.
相关试题

