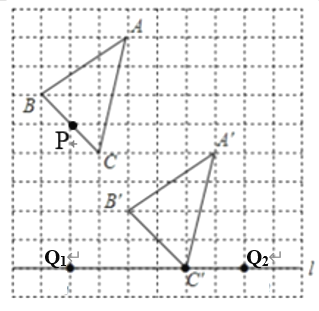
【题目】如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△A'B'C',点C的对应点是直线上的格点C'.
(1)画出△A'B'C';
(2)在BC上找一点P,使AP平分△ABC的面积;
(3)试在直线l上画出所有的格点Q,使得由点A'、B'、C'、Q四点围成的四边形的面积为9.

参考答案:
【答案】(1)所求△A'B'C'如图所示,详见解析;(2)点P的位置如图所示,详见解析;(3) 格点Q的位置如图所示,详见解析.
【解析】
(1)画出A、B、C的对应点A'、B'、C',顺次连接A'、B'、C'即可;
(2)根据等底同高的两个三角形面积相等即可判断点P是BC的中点;
(3)分两种情况分别求解即可.
(1)如图所示,已知C'的位置,根据平移的性质可确定A'、B'的位置,顺次连接A'、B'、C',
(2)如图所示,点P是线段BC的中点.
设△ABC的高为h,
∵点P在线段BC上,要使AP平分△ABC的面积,即S△ABP=S△ACP,
∴![]() BP×h=
BP×h=![]() CP×h,
CP×h,
∴BP=CP,
∴点P是BC的中点;
(3)由题意可知:S△A'B'C'=5,
∴当S△Q1B'C'=4或S△Q2A'C'=4时即可,
∵B'、A'到直线l的距离分别是2、4,
∴Q1C' =4, C'Q2=2,
如图,点Q1,Q2即为所求.
-
科目: 来源: 题型:
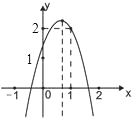
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1 , x2 , 其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b<0,b2+8a>4ac,a<﹣1,其中结论正确的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
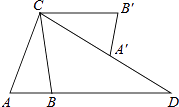
查看答案和解析>>【题目】如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某段铁路两旁安置了两座可旋转探照灯,主道路是平行,即PQ∥MN. 如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度. 若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动_________秒,两灯的光束互相平行.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(m+1)x2-|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
-
科目: 来源: 题型:
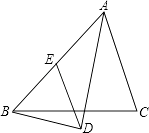
查看答案和解析>>【题目】在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
相关试题

