【题目】张老师抽取了九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,规定x≥6.25为合格,x≥9.25为优秀.并绘制出扇形统计图和频数分布直方图(不完整).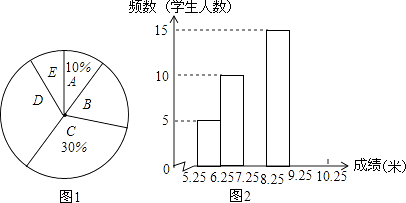
(1)抽取的这部分男生有人,请补全频数分布直方图;
(2)抽取的这部分男生成绩的中位数落在组?扇形统计图中D组对应的圆心角是多少度?
(3)如果九年级有男生400人,请你估计他们掷实心球的成绩达到合格的有多少人?
参考答案:
【答案】
(1)50
(2)C解:∵D组有15人,占 ![]() ×100%=30%,∴对应的圆心角=360°×30%=108°
×100%=30%,∴对应的圆心角=360°×30%=108°
(3)解:(1﹣10%)×400=360人,
估计他们掷实心球的成绩达到合格的有360人
【解析】解:(1)设抽取的这部分男生有x人.则有 ![]() ×100%=10%,
×100%=10%,
解得x=50,
C组有50×30%=15人,D组有50﹣5﹣10﹣15﹣15=5人,
条形图如图所示:
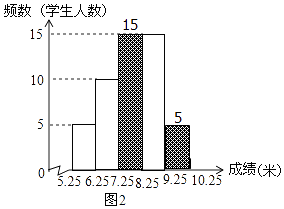
⑵抽取的这部分男生成绩的中位数落在C组.
所以答案是C.
【考点精析】认真审题,首先需要了解频数分布直方图(特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图)),还要掌握扇形统计图(能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=α.∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠A2019BC与∠A2019CD的平分线相交于点A2020,得∠A2020,则∠A2020=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,O为原点,已知A(1,1),在坐标轴上确定点P,使△AOP为等腰三角形,则符合条件的点P有_____个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,长方形纸片ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合.
求:(1)折叠后DE的长;(2)以折痕EF为边的正方形面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
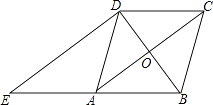
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长. -
科目: 来源: 题型:
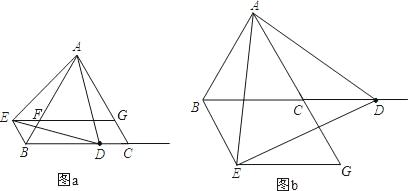
查看答案和解析>>【题目】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
(1)如图(a)所示,当点D在线段BC上时.
①求证:△AEB≌△ADC;
②探究四边形BCGE是怎样特殊的四边形?并说明理由;
(2)如图(b)所示,当点D在BC的延长线上时,直接写出(1)中的两个结论是否成立;
(3)在(2)的情况下,当点D运动到什么位置时,四边形BCGE是菱形?并说明理由.
相关试题

